Regulatorul de încărcare

Convertorul c.c. - c.c.

În multe aplicații industriale este necesar de a converti/modifica valoarea unei tensiuni de c.c. (curent continuu), a unei surse, într-o altă tensiune tot de c.c. dar cu altă valoare, ce poate fi variabilă sau fixă.

Un convertor de c.c. poate converti direct din c.c. în c.c. Un convertor de c.c. poate fi asimilat, prin analogie, cu un transformator de c.a. (curent alternativ) ce are factorul de transformare variabil. Ca și transformatorul, convertorul de c.c. - c.c., poate fi folosit la scăderea sau creșterea tensiunii de ieșire în comparație cu tensiunea de intrare¹ .

Convertoarele de c.c. sunt folosite în următoarele domenii:

la tracțiuni, la reglajul vitezei de rotație a motoarelor/servomotoarelor;
energiilor neconvenționale, la încărcarea bateriilor;
etc..

În funcție de modificarea tensiunii de ieșire în raport cu tensiunea de intrare, în convertorul de c.c., acestea se pot clasifica în:

convertor de c.c. coborâtor, în engleză denumit buck converter;
convertor de c.c. ridicător, în engleză denumit boost converter;
convertor de c.c. coborâtor-ridicător, în engleză denumit buck-boost converter.

Aceste trei tipuri de convertoare sunt neizolate, adică tensiunea de intrare și cea de ieșire împărtășesc un punct comun. Există și variații izolate ale acestor topologii de convertoare. Topologia convertorului se referă la modul în care sunt conectate elementele întreruptoare (tranzistorul, dioda, etc.), bobina și condensatorul de ieșire. Fiecare topologie are proprietăți unice. Aceste proprietăți includ: rapoartele de conversie/transformare a tensiunilor, natura curenților de intrare respectiv de ieșire și caracteristica de riplu a tensiunii de ieșire. O altă importantă proprietate este răspunsul în frecvență a funcției de transfer a tensiunii de ieșire¹ .

În cele ce urmează voi prezenta cele trei tipologii ale convertoarelor de c.c. cu tensiunea ieșire neizolată.

Convertorul de c.c. coborâtor - de tip Buck¹

Cea mai comună și probabil cea mai simplă topologie este de tip coborâtoare, numită și topologie de tip Buck.
Proiectanții de surse de alimentare aleg această topologie când este necesar ca tensiunea de ieșire (sau cea necesară/dorită) este mai mică ca cea de intrare iar tensiunea de ieșire nu trebuie să fie izolată de cea de intrare.

Curentul ce intră într-o astfel de topologie, dinspre sursă, este discontinuu sau pulsator datorită întrerupătorului, \(Q1\), curent ce pulsează de la \(0\) la \(I_O\) la fiecare ciclu de comutare.
Curentul de ieșire, pentru un etaj de tip Buck, poate fi continuu sau nepulsator (fără trecere prin zero), deoarece curentul de ieșire este furnizat de combinația bobină-condesator de ieșire, unde condensatorul de ieșire nu contribuie niciodată la curentul de ieșire.

În figura de mai jos, Figura 1, este arătat simplificat schema unui etaj de tip Buck cu un bloc de comandă inclus.

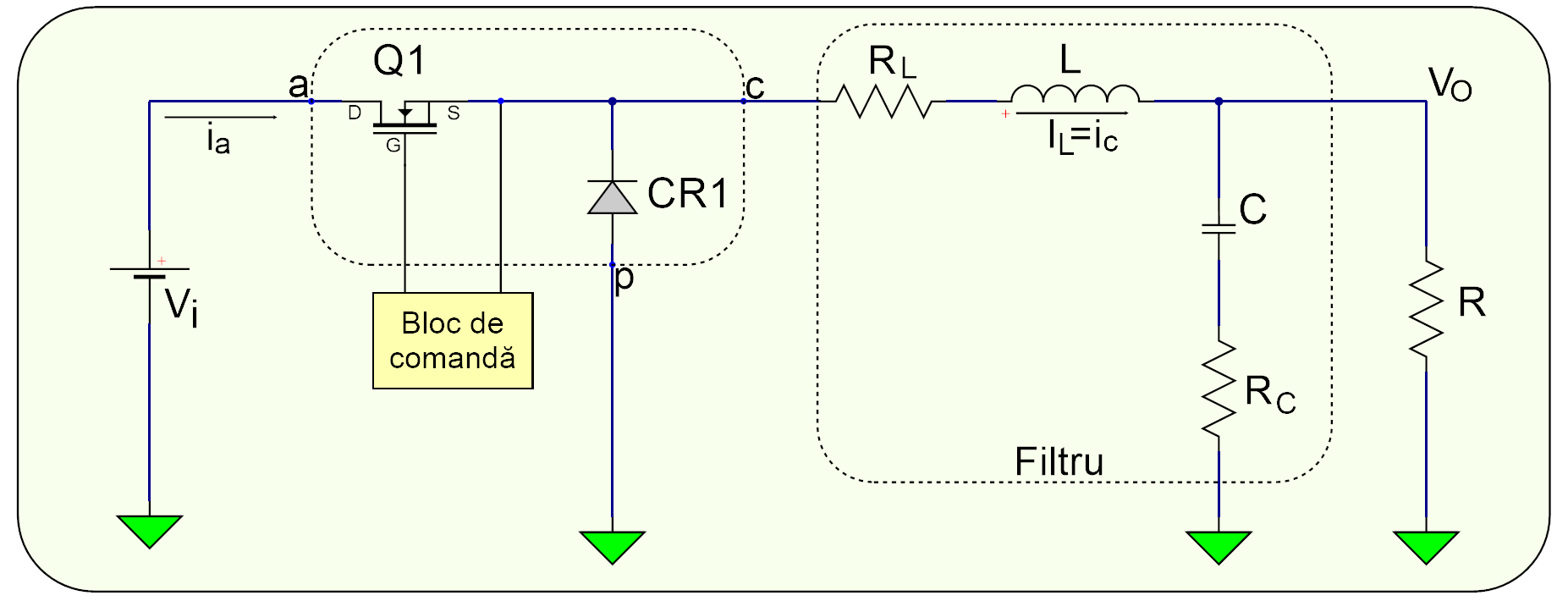
Etajul_Buck
Figura 1. Schema electrică a unui convertor de c.c. de tip Buck.

Pentru analiză voi folosi un program de tip CAD, numit LTspice a celor de la Analog Devices.
Întrerupătorul de putere, \(Q1\), este un tranzistor MOSFET cu canal N, dioda, \(CR1\), este denumită de obicei diodă de captură sau liberă. Bobina \(L\) și condensatorul \(C\) formează filtrul de ieșire.

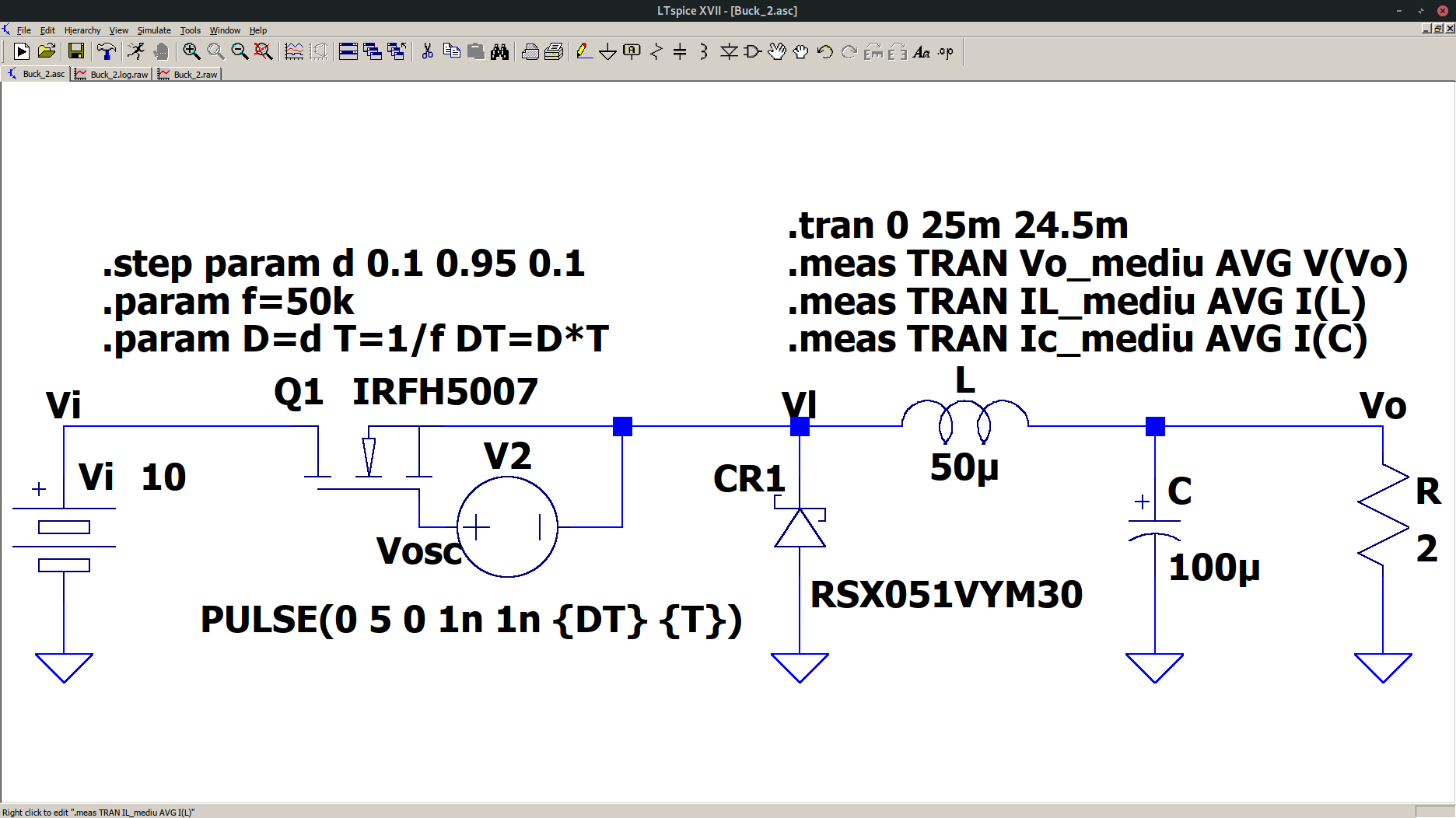
Figura 1a. Schema electrică a unui convertor de c.c. de tip Buck, in vederea simulării cu LTspice.

Fișierul netlist al circuitului din Figura 1a este prezentat mai jos:

* C:\users\florin\Documentele mele\LTspiceXVII\Buck\Buck_2\Buck_2.asc
Vi Vi 0 10
L Vl Vo 50µ Ipk=7 Rser=0.02 Rpar=38000 Cpar=5.86p mfg="Gowanda" pn="894AT5002V"
C Vo 0 100µ V=25 Irms=370m Rser=0.24 Lser=0 mfg="Nichicon" pn="UPL1E101MPH" type="Al electrolytic"
R Vo 0 2
D§CR1 0 Vl RSX051VYM30
V2 Vosc Vl PULSE(0 5 0 1n 1n {DT} {T})
M§Q1 Vi Vosc Vl Vl IRFH5007
.model D D
.lib C:\users\florin\Documentele mele\LTspiceXVII\lib\cmp\standard.dio
.model NMOS NMOS
.model PMOS PMOS
.lib C:\users\florin\Documentele mele\LTspiceXVII\lib\cmp\standard.mos
.tran 0 25m 24.5m
.param D=d T=1/f DT=D*T
.step param d 0.1 0.95 0.1
.param f=50k
.meas TRAN Vo_mediu AVG V(Vo)
.meas TRAN IL_mediu AVG I(L)
.meas TRAN Ic_mediu AVG I(C)
.backanno
.end

Rezultatul simulării, circuitului de mai sus, este prezentat în imaginea de mai jos, Figura 2.

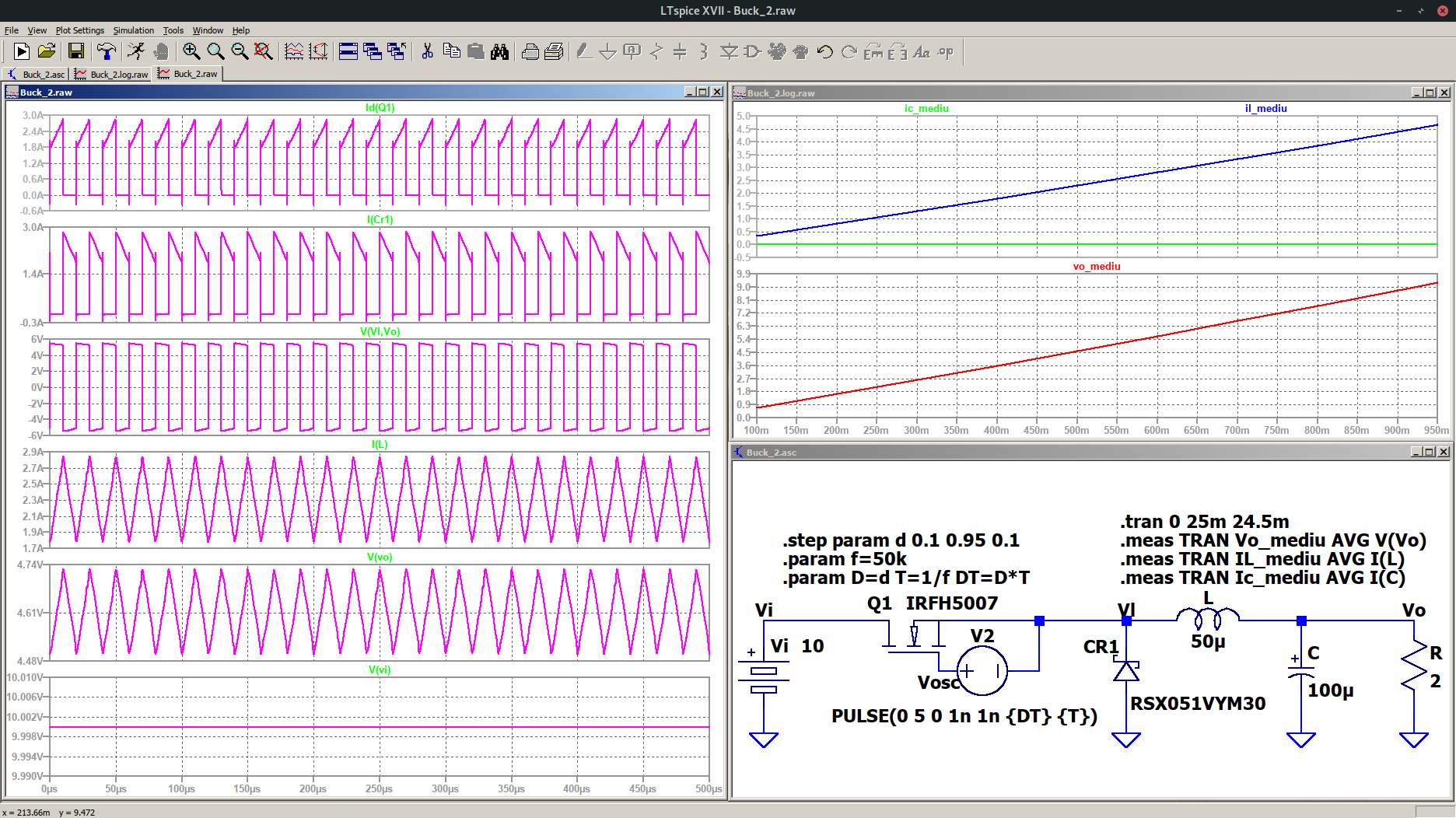
Figura 2a. Formele de undă rezultate în urma simulării convertorului de c.c. de tip Buck, de la Figura 1, pentru \(D=0,5\).

În Figura 3a , caracteristica \(ESR\) a condensatorului, \(C\), este echivalată cu rezistența în serie, \(Rc\), cu acesta iar rezistența echivalentă în c.c. a bobinei, \(L\), este echivalată cu rezistență montată în serie cu aceasta, fiind notată cu \(RL\). Rezistorul, \(R\), reprezintă sarcina văzută de către convertorul de tip Buck.
Pentru simplificare tranzistorul, \(Q1\), a fost înlocuit cu un întrerupător comandat în tensiune și sa ținut cont de rezistența în conducție, \(RDS\), a tranzistorului ce a fost montată în serie cu întrerupătorul. Schema este echivalentă, din punct de vedere electric, cu schema din Figura 1.

Fișierul netlist al circuitului din Figura 3a este următorul:

* C:\users\florin\Documentele mele\LTspiceXVII\Buck.asc
S§Q1 Vl N001 Vosc 0 SW_Q1
Vi Vi 0 10
L N002 Vo 50µ
C Vo N003 100µ
R Vo 0 2
D§CR1 0 Vl RBR20BM30A
V2 Vosc 0 PULSE(0 1 0 0 0 {DT} {T})
RL N002 Vl 0.02
RDS Vi N001 5.9m
Rc N003 0 0.24
.model D D
.lib C:\users\florin\Documentele mele\LTspiceXVII\lib\cmp\standard.dio
.tran 0 10m 9.5m
.model SW_Q1 SW(Ron=0.1 Roff=1Meg Vt=.5 Vh=-.4)
.param D=d T=1/f DT=D*T
.step param d 0.1 0.95 0.1
.param f=50k
.meas TRAN Vo_mediu AVG V(Vo)
.meas TRAN IL_mediu AVG I(L)
.meas TRAN Ic_mediu AVG I(C)
.backanno
.end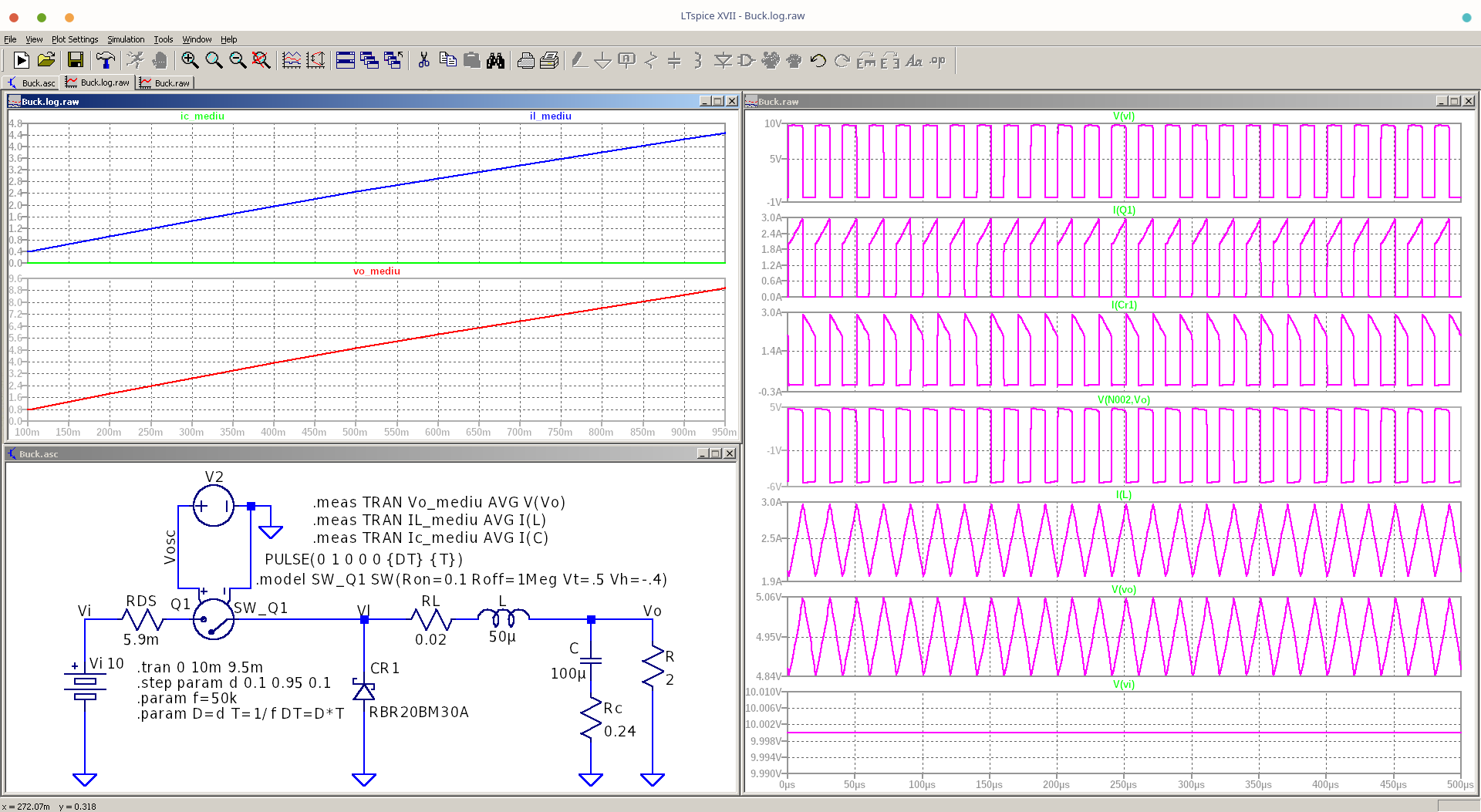

Figura 3a. Formele de undă rezultate în urma simulării convertorului de c.c. de tip Buck, de la Figura 1, pentru \(D=0,5\).

În timpul funcționării normale a convertorului c.c. - c.c., de tip Buck, întrerupătorul \(Q1\) este comandat pe poziția închis, respectiv deschis de către circuitul/blocul de comandă. Acesta acțiune a circuitului/blocului de comandă asupra întrerupătorului determina apariția unui tren de impulsuri la intersecția celor trei elemente \(Q1\), \(CR1\) și \(L\) care este filtrat de către filtrul de ieșire \(L-C\) pentru a produce o tensiune continuă de ieșire, \(V_o\).

Analiza în regim static (steady state) a convertorului c.c. - c.c. coborâtor (de tip Buck)

Un astfel de convertor poate funcționa în modul curent discontinuu sau continuu (funcție de curentul prin bobina \(L\)).
Modul curent continuu este caracterizat de circulația continuă a curentului prin bobina \(L\) pe durata întregului ciclu de comutație.
Modul curent discontinuu este caracterizat de circulația întreruptă a curentului prin bobina \(L\), cu treceri prin zero. Acest mod este caracterizat prin faptul că, curentul prin bobină este zero pentru o porțiune a ciclului de comutare. Începe de la zero, atinge o valoare maximă și revine la zero în timpul fiecărui ciclu de comutare.
Pentru acestă analiză este folosit un tranzistor MOSFET cu canal N, ce este comandat cu tensiune pozitivă \(V_{GS(ON)}\), aplicată pe poarta \(G\) și sursa \(S\) a tranzistorului/întrerupătorului \(Q1\) de către circuitul de comandă ce comandă pe poziția \(ON\) acest întrerupător/tranzistor \(Q1\). Avantajul acestui tranzistor MOSFET cu canal N, este că are mică rezistența în conducție \(R_{DS(ON)}\), dar circuitul de comandă este mai complicat. În cazul tranzistorului de tip MOSFET cu canal P ce are, în general, o rezistență în conducție \(R_{DS(ON)}\) mai ridicată, circuitul de comandă este mai simplu.
Tranzistorul \(Q1\) și dioda \(CR1\) sunt desenate, în Figura 1, în chenarul cu linie punctată, cu terminalele etichetate a, p și c. Curentul prin bobina \(L\) notat cu \(I_L\), este același cu curentul ce iese prin terminalul notat c, respectiv curentul \(i_c\).

Analiza în modul curent continuu a convertorului c.c. - c.c. coborâtor (de tip Buck)

În cele urmează se descrie funcționarea etajului de tip Buck, în regim static (steady state), în modul curent continuu de funcționare (\(I_L>0\)).
Principalul rezultat al acestei analize este dependența tensiunii de ieșire \(V_o\) față de factorul de umplere \(D\) și a tensiunii de intrare \(V_i\).
Regimul static (steady state) implică faptul că tensiunea de intrare, tensiunea de ieșire, curentul de ieșire prin sarcină și factorul de umplere sunt fixe și nu variază. În general literele cu majusculă sunt atribuite numelor variabilelor pentru a indica o cantitate aflată în stare statică.

În modul de conducție continuu, etajul de tip Buck presupune două stări de comutare pe durata unui ciclu.

STAREA ON - atunci când tranzistorul/întrerupătorul, \(Q1\), este \(ON\) și \(CR1\) este \(OFF\);
STAREA OFF - atunci când tranzistorul/întrerupătorul, \(Q1\), este \(OFF\) și \(CR1\) este \(ON\).

Un circuit simplu liniar poate reprezenta fiecare stare în care elementele \(Q1\) și \(CR1\) sunt înlocuite cu circuitele lor echivalente aferente fiecărei stări \(ON\) sau \(OFF\).

Schemele electrice echivalente fiecărei stări sunt prezentate în figura de mai jos, Figura 2.
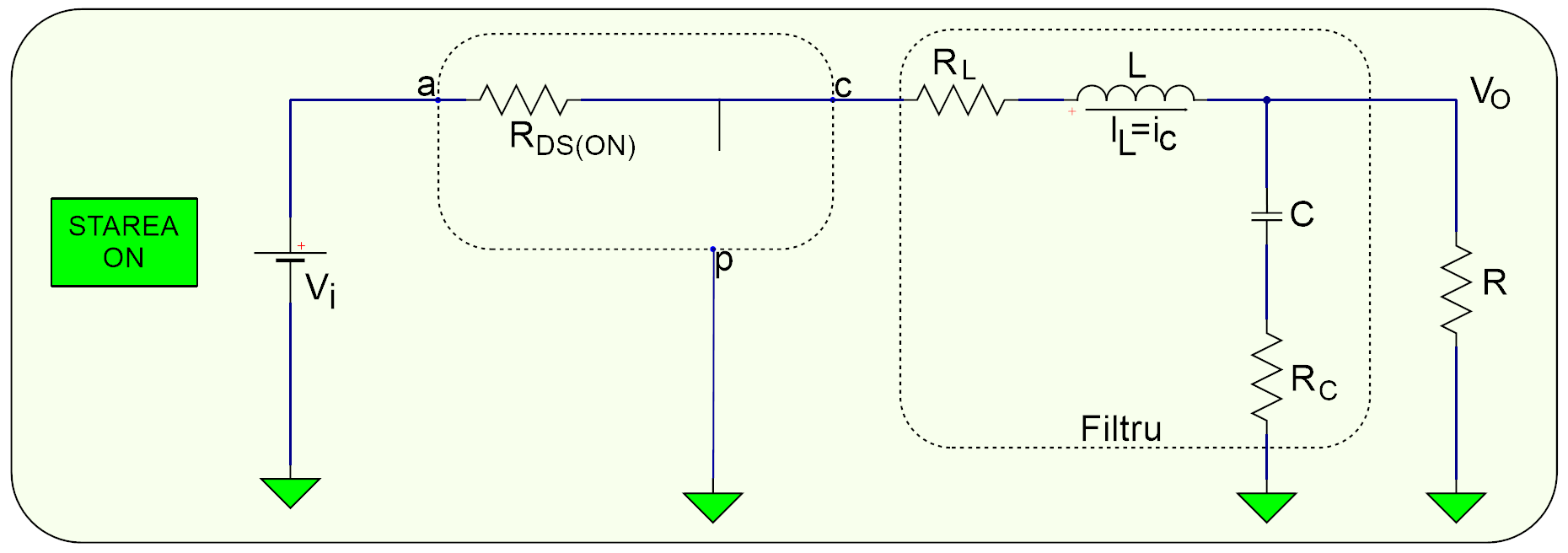
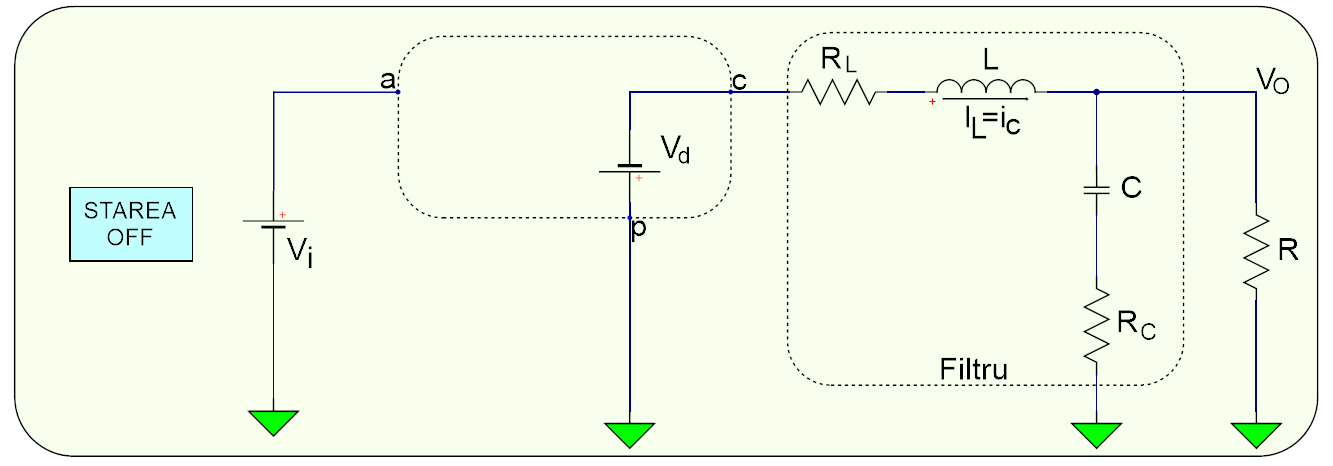
Figura 2. Stările \(ON\) și \(OFF\) a etajului de tip Buck.

Durata de timp a stării \(ON\) este:

\[ {T_{ON}}={D} \times {T_S}\]

, unde \(D\) este factorul de umplere, impus de blocul de comandă, exprimat ca raport al timpului când întrerupătorul este \(ON\) la durata de timp a întregii perioade, \(T_S\):

\[ {D} = {{T_{ON}} \over {T_{S}}}\]

Durata de timp, pentru starea \(OFF\) este notată \(T_{OFF}\). Astfel avem numai două stări pe durata unui ciclu complet (o perioadă) pentru modul curent continuu. Durata stării \(OFF\) este:

\[ T_{OFF}=(1-D) \times T_S\]

, unde \((1-D)\) este notat uneori cu \(D'\).

Aceste cicluri de timp sunt prezentate în Figura 3.
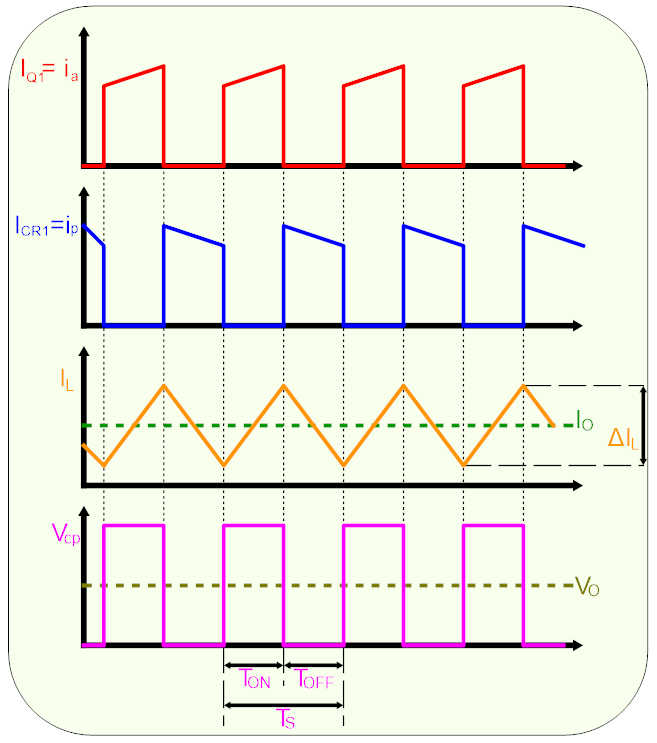
Forme unda convertor Buck
Figura 3. Formele de undă în modul de conducție continuu, \(I_L>0\).

Dacă ne uităm la Figura 2, în timpul stării \(ON\), observăm că:

\(Q1\) prezintă o rezistență scăzută, \(R_{DS(ON)}\), de la drena \(D\) către sursa \(S\) și are o mică cădere de tensiune:
\[ V_{DS}=I_{L} \times R_{DS(ON)}\]
Există de asemnea, o cădere mică de tensiune pe rezistență în c.c. a bobinei egală cu:
\[ V_{RL}=I_L \times R_L\]

Astfel tensiunea de intrare, \(V_i\), minus pierderile (\(V_{DS}+V_{RL}\)), este aplicată în partea stângă a bobinei, \(L\). \(CR1\) este \(OFF\) în tot acest timp deoarece tensiunea aplicată este inversă. Tensiunea aplicată în partea dreaptă a bobinei \(L\) este pur și simplu tensiunea de ieșire \(V_o\).
Curentul prin bobină, \(I_L\), curge de la sursa de intrare, \(V_i\), prin \(Q1\) către combinația condensator de ieșire, \(C\) și rezistența de sarcină, \(R\). În timpul stării \(ON\), tensiunea aplicată pe bobină, \(V_L\), este constantă și egală cu:

\[ V_L=V_i-V_{DS}- V_{RL} - V_o\]

Adoptând convenția de polaritate pentru curentul \(I_L\) prezentată în Figura 2, curentul prin bobină crește ca urmare a tensiunii aplicate. De asemenea deoarece tensiunea aplicată este în esență constantă, curentul prin bobină crește liniar.
Această creștere a curentului prin bobină în timpul \(T_{ON}\) este ilustrat în figura 3.

\[ {V_L}={L} \times {{di} \over {dt}} \Rightarrow \Delta I_L = {V_L \over L} \times \Delta T\]

Creșterea curentului prin circuit, pe durata stării \(ON\), este dată de:

\[ \Delta I_L(+) = {(V_i - V_{DS} - V_{RL}) -V_O \over L} \times T_{ON}\]

Valoarea \(\Delta I_L(+)\) este riplu de curent prin bobină.

Dacă ne uităm la Figura 2, atunci când \(Q1\) este \(OFF\), acesta prezintă o impedanță ridicată între drena \(D\) și sursa \(S\). De aceea, deoarece curentul care circulă prin bobina L nu se poate schimba instantaneu, curentul trece de la tranzistorul \(Q1\) la dioda \(CR1\). Odată cu scăderea curentului prin bobină, tensiunea pe bovină își inversează polaritatea până când dioda \(CR1\) devine polarizată direct și intră în conducție (\(ON\)).
Tensiunea în partea stângă a bobinei, \(L\), devine \(-(V_d+V_{RL})\), unde cantitativ , \(V_d\), reprezintă căderea de tensiune pe dioada \(CR1\).
Tensiunea în partea dreaptă a bobinei, \(L\), rămâne a fi tensiunea de ieșire, \(V_O\).
Curentul prin bobină, \(I_L\), curge acum de la masă, prin dioda, \(CR1\), către ieșirea realizată din condensatorul \(C\) și rezistența de sarcină \(R\).
În timpul stării \(OFF\), magnitudinea aplicată pe bobina \(L\) este:

\[ V_L = V_O+V_d+V_{RL}\]

Menținând aceeași convenție de polaritate, acestă tensiune aplicată este negativă (sau opusă ca polaritate cu tensiunea aplicată în starea \(ON\)).
Prin urmare curentul prin bobină scade, în timpul stării \(OFF\).
De asemenea, deoarece tensiunea aplicată este în esență constantă, curentul prin bobină \(I_L\) va scade liniar. Acestă scădere a curentului \(I_L\) prin bobină în timpul stării \(OFF\) este prezentat de asemenea în Figura 3.
Curentul prin bobină, pe durata stării \(OFF\), va scade în conformitate cu relația:

\[ \Delta I_L(-)={{V_O+(V_d+V_{RL}) \over {L}} \times T_{OFF}} \]

Valoarea \(\Delta I_L(-)\) este de asemenea riplu de curent prin bobină.

În regim staționar (steady state), curentul \(\Delta I_L(+)\) crește, pe durata stării \(ON\) și respectiv curentul \(\Delta I_L(-)\) scade, pe durata stării \(OFF\). Aceste valori trebuie să fie egale. Altfel, valoarea curentului va crește sau va scădea în valori nete, de la un ciclu la altul și atunci nu mai suntem în cazul unui regim staționar (steady state).
De aceea, aceste două ecuații pot fi egalizate și rezolvate pentru \(V_O\) pentru a obține relația de transformare/conversie a tensiunii de ieșire \(V_O\) pentru modul de conducție continuu.
Rezolvând:

\[ V_O=(V_i-V_{DS}) \times {T_{ON} \over {T_{ON} + T_{OFF}}}-V_d \times {T_{OFF} \over {T_{ON} + T_{OFF}}} - V_{RL}\]

, unde:

\[ \left.\begin{matrix} {T_S=T_{ON}+T_{OFF}} \\ {D={T_{ON} \over T_S}} \\ {(1-D) = {T_{OFF} \over T_S}} \end{matrix}\right\} \Rightarrow V_O=(V_i-V_{DS}) \times D - V_d \times (1-D)-V_{RL}\]

În ecuațiile de mai sus ale \(\Delta I_L(+)\) și \(\Delta I_L(-)\), tensiunea de ieșire, \(V_O\), în c.c. a fost implicit presupusă a fi constantă, fără riplu de tensiune pe durata \(ON\) sau \(OFF\).
Aceasta este o simplificare și implică două ipoteze separate:

în primul rând, se presupune condensatorul de ieșire, \(C\), ca fiind suficient de mare astfel încât riplu/schimbarea de tensiune este neglijabilă;
în al doilea rând, se presupune căderea de tensiune pe ESR (rezistența serie echivalentă \(R_C\)) este de asemenea neglijabilă.

Aceste ipoteze sunt valabile, deoarece valoarea riplului de tensiune este proiectată a fi mult mai mică decât valoarea tensiunii de ieșire, \(V_O\), în c.c..
Relația factorului de transformare a tensiunii de ieșire \(V_O\), de mai sus, ilustrează faptul că \(V_O\) poate fi modificată prin ajustarea/modificarea duratei de ciclu \(D\) - numit și factor de umplere - și este întotdeauna mai mică decât tensiunea de intrare \(V_i\) deoarece \(D\) satisface condiția \(0>D<1\).
O altă simplificare folosită este a considera \(V_{DS}\), \(V_d\) și \(R_L\) implicit și \(V_{RL}\) suficient de mici pentru a fi ignorate, astfel:

\[ \left.\begin{matrix} V_{DS}=0 \\ V_d = 0 \\ V_{RL} = 0 \end{matrix}\right\} \Rightarrow V_O = V_i \times D \Rightarrow D={V_O \over V_i}\]

Un alt mod simplificat de analiză a funcționării circuitului este considerarea filtrului de ieșire ca fiind o rețea de mediere. Aceasta este o simplificare validă deoarece frecvență de tăiere a filtrului (de obicei între \(50[Hz]\) și \(5[kHz]\)) este întotdeauna mai mică decât frecvența de comutare a sursei de alimentare de către \(Q1\) (de obicei între \(100[Hz]\) și \(500[kHz]\)).
Tensiunea de intrare aplicată pe filtru este tensiunea la joncțiunea \(Q1\), \(CR1\) și \(L\), notată \(V_{c-p}\).
Curentul prin bobină este egal cu curentul de ieșire deoarece curentul prin condensator este zero.
Matematic avem:

\[ I_{L(med)} = I_O\]

Analiza în modul curent discontinuu a convertorului de c.c. - c.c. coborâtor (de tip Buck)

În cele ce urmează se va analiza ce se întâmplă atunci când curentul prin sarcină este scăzut. Mai întâi observăm, așa cum s-a arătat mai sus, că etajul de tip Buck are curentul de ieșire \(I_O\) ca fiind media curentului prin bobină \(I_{L(med)}\).
Acest lucru este evident deoarece curentul \(I_L\) circulă prin bobină \(L\) spre condensatorul \(C\) și rezistență de sarcină \(R\), iar media curentului prin condensator este zero.
Dacă curentul prin sarcina de ieșire este redus, sub nivelul critic, curentul prin bobină va fi zero pentru o porțiune a ciclului de comutare. Acest lucru ar trebui să fie evident din formele de undă prezentate în Figura 3, deoarece amplitudinea vârf la vârf a riplului de curent \(\Delta I_L\) nu se modifică cu curentul de ieșire prin sarcină. Într-un convertor/etaj de tip Buck dacă curentul prin bobină \(I_L\) încercă să scadă sub zero se va opri la zero (datorită curgerii unidirecționale a curentului prin dioda \(CR1\)) și rămâne acolo până la începutul unui nou ciclu de comutare.
Acest mod operare se numește mod conducție discontinuu. Un convertor/etaj de tip Buck ce operează în acest mod de conducție discontinuu are trei stări unice în timpul fiecărui ciclu de comutare, spre deosebire de cele două stări pentru modul de conducție continuu.
Starea curentului de sarcină în cazul în care convertorul/etajul de tip Buck este la limita dintre modul de conducție continuu și discontinuu este arătată în Figura 4. Se observă cum curentul prin bobină cade la zero și ciclu următor de comutare începe imediat după ce curentul ajunge la zero.
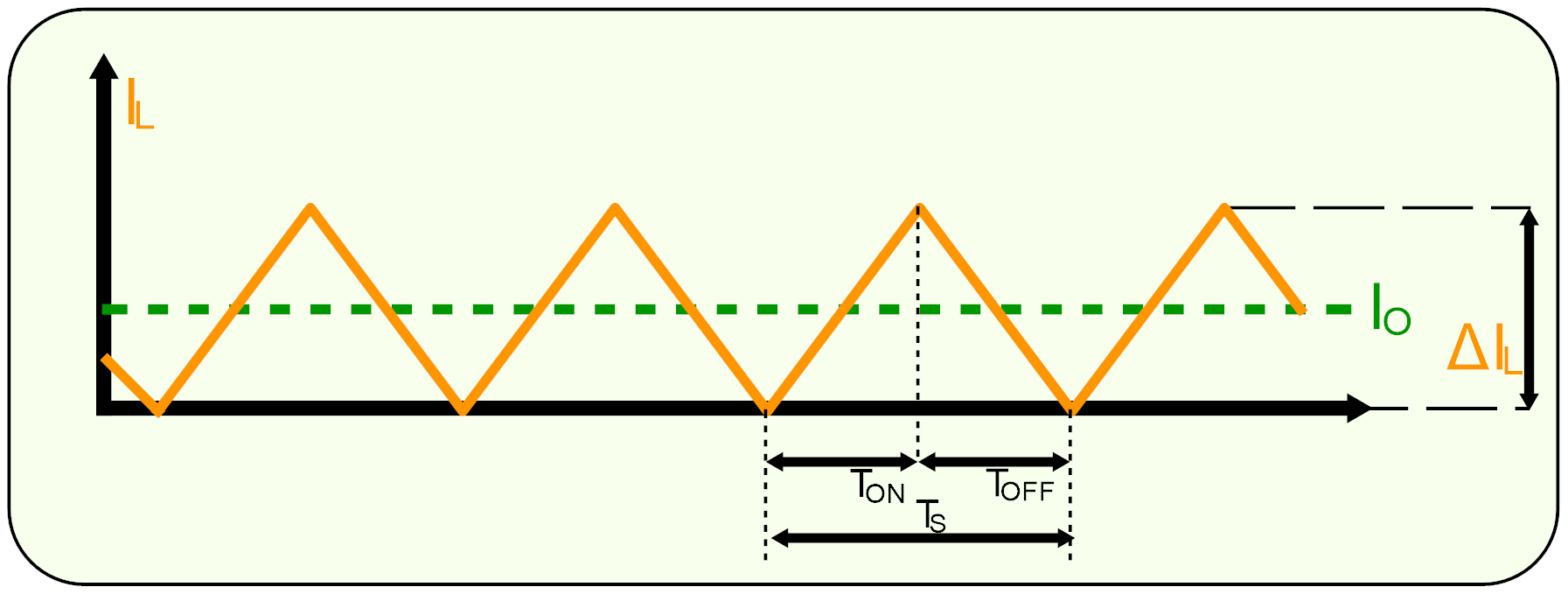
Limita dintre modul de conductie continuu si discontinuu
Figura 4. Limita dintre modul de conducție continuu și discontinuu.

Scăderea suplimentară a curentului de ieșire pune convertorul/etajul de tip Buck în modul de conducție discontinuu. Acest mod de conducție este ilustrat în Figura 5. Răspunsul în frecvență a convertorului/etajului de tip Buck în modul de conducție discontinuu este destul de diferit de răspunsul in frecvență în modul de conducție continuu. De asemenea, relația intrare-ieșire este destul de diferită, după cum se arată în cele ce urmează.

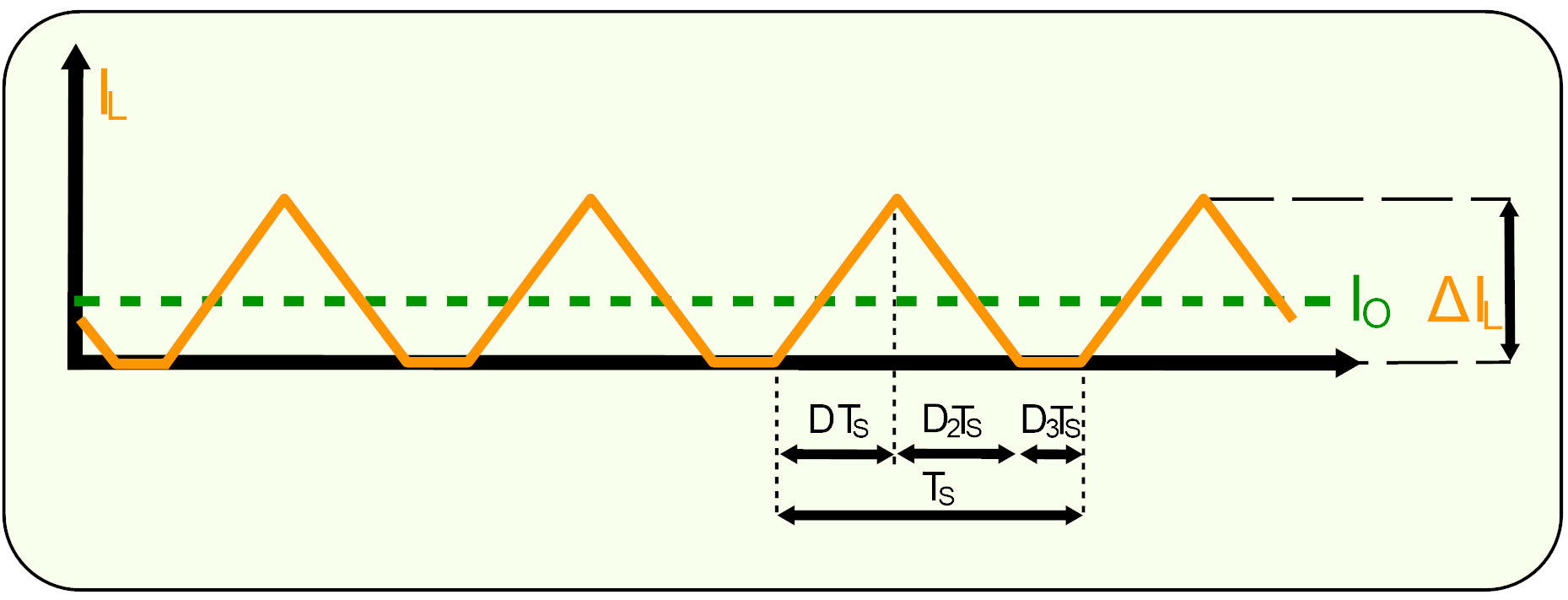
Curentul in modul de conducție discontinuu

Figura 5. Modul de conducție discontinuu.

Înainte de a determina raportul de transformare/conversie a modului de conducție discontinuu, observăm că există trei stări unice pe care convertorul/etajul de tip Buck le realizează în timpul funcționării a modului discontinuu a curentului:

Starea \(ON\) este atunci când \(Q1\) este \(ON\) și \(CR1\) este \(OFF\);
Starea \(OFF\) este atunci când \(Q1\) este \(OFF\) și \(CR1\) este \(ON\);
Starea \(IDLE\) (așteptare) este atunci când \(Q1\) este \(OFF\) și \(CR1\) este \(OFF\);

Primele două stări sunt identice cu cele ale modului de conducție continuu și circuitele din Figura 2 sunt aplicabile mai puțin \(T_{OFF} \neq (1-D) \times T_S\). Restul de timp rămas este starea \(IDLE\). În plus vom putea omite: rezistența în c.c. \(R_L\) a bobinei/inductorului \(L\) implicit și căderea de tensiune pe aceasta \(V_{RL}\), căderea de tensiune pe diodă \(V_d\) și căderea de tensiune \(V_{DS}\) pe tranzistorul \(Q1\) în starea \(ON\), deoarece sunt suficient de mici pentru a le considera zero/nule.
Ecuațiile pentru creșterea curentului, \(\Delta I_L(+)\), prin bobina/inductorul \(L\) pe durata stării \(ON\) și ecuațiile pentru descreșterea curentului, \(\Delta I_L(-)\), prin bobina/inductorul \(L\) pe durata stării \(OFF\) sunt determinate în cele ce urmează.
Astfel, creșterea curentului \(\Delta I_L(+)\) prin bobina/inductorul \(L\), în timpul stării \(ON\), este dată de:

\[ \Delta I_L(+)={{V_i-V_O} \over L} \times {T_{ON}} = {{V_i-V_O} \over L} \times {D \times T_S} = I_{pk}\]

Magnitudinea riplului de curent, \(\Delta I_L(+)\), este de asemenea vârful de curent, \(I_{pk}\), deoarece în modul de conducție discontinuu, curentul pornește de la zero la începutul fiecărui ciclu.

Scăderea curentului \(I_L\) prin bobina \(L\), în timpul stării \(OFF\), este dată de:

\[ \Delta I_L(-)={{V_O} \over L} \times {T_{OFF}}\]

Ca si în cazul modului de conducție continue curentul crește, \(\Delta I_L(+)\), în timpul duratei \(ON\) și curentul scade \(\Delta I_L(-)\) în timpul duratei \(OFF\). și aceste creșteri respectiv scăderi ale curentului sunt egale.
Prin urmare aceste două ecuații pot fi egalizate și rezolvate, scoțând \(V_O\), pentru a obține prima dintre cele două ecuații care trebuie folosite pentru a rezolva raportul de conversie/transformare a tensiunilor:

\[ V_O=V_i \times {T_{ON} \over {T_{ON} +T_{OFF}}}=V_i \times {D \over {D+D_2}}\]

Curentul de ieșire, \(I_O\), (tensiunea de ieșire \(V_O\) împărțită la sarcina de ieșire \(R\)), este valoarea medie a curentului, \(I_L\), prin bobina \(L\):

\[ I_O=I_{L(med)}={V_O \over R} = {I_{pk} \over 2} \times {{D \times T_S + D_2 \times T_S} \over T_S} \]

Înlocuind în ecuația de mai sus \(I_{pk}\) determinat mai devreme, va rezulta:

\[ I_O={V_O \over R} = (V_i-V_O) \times {{D \times T_S} \over {2 \times L}} \times (D+D_2)\]

Astfel am obținut două ecuații, cea pentru curentul de ieșire, \(I_O\), și cea pentru tensiunea de ieșire, \(V_O\), amândouă cu termenii \(V_i\), \(D\) și \(D_2\).
Rezolvând acum fiecare ecuație pentru \(D_2\) și egalăm cele două ecuații obținute. Ecuația rezultată, o expresie pentru tensiunea de ieșire, \(V_O\).
Relația de conversie/transformare a tensiunii în modul de conducție discontinuu este dată de:

\[ V_O=V_i \times {2 \over {1+ \sqrt {1+{{4 \times K} \over D^2}}}}\]

, unde:

\[ K = {{2 \times L} \over {R \times T_S}}\]

Relația de mai sus prezintă una dintre diferențele majore dintre cele două moduri de conducție. Pentru modul de conducție discontinuu, relația de transformare a tensiunii de ieșire, \(V_O\), este o funcție a tensiune de intrare, \(V_i\), duratei ciclului (factorului de umplere), \(D\), inductanței \(L\), frecvenței de comutare \(T_S\) și a rezistenței de sarcină \(R\), în timp ce pentru modul de conducție continuu relația de transformare/conversie a tensiunii de ieșire depinde numai de tensiunea de intrare, \(V_i\), și factorul de umplere (durata ciclului), \(D\).
Trebuie remarcat faptul că starea de funcționare a unui convertor/etaj de tip Buck, în situații normale, este arareori în modul de comutație discontinuă, dar acest mod de conducție poate apărea oricând ca urmare a scăderii curentului de sarcină/ieșire sub un anumit nivel critic.

Modul de conductie discontinuu
Figura 6. Formele de undă în modul de conducție discontinuu

Inductanță critică

Analizele anterioare, ale etajului de tip Buck, au fost pentru modurile de conducție continuu și discontinuu în regim static.
Modul de conducție al etajului este o funcție a tensiunii de intrare, tensiunii de ieșire, curentului de ieșire și a valorii inductanței aferente bobinei de la ieșire.
Un etaj de tip Buck poate fi proiectat să funcționeze în regim continuu, pentru curenți de sarcină peste un anumit nivel, de obicei 5%-10% din valoarea maximă.
De obicei, intervalul tensiunii de intrare, tensiunea de ieșire și curentul de sarcină sunt parametri impuși (definiți) ale etajului de tip Buck, urmând ca valoarea inductorului să fie un parametru ce urmează a fi determinat astfel încât să fie menținut mediul de regim continuu.
Valoarea minima a inductorului pentru a menține regimul de conducție continuu poate fi determinată urmând următorul algoritm.
Pentru început definim \(I_{O(crit)}\) ca fiind curentul minim pentru care încă se poate menține modul de funcționare continuu, prezentat în figura 4 și care poate fi calculat astfel:

\[ I_{O(crit)}= {{\Delta I_L} \over {2}}\]

După care determinăm inductanța minimă a bobinei (inductorului) care să satisfacă relația de mai sus, astfel:

\[ L_{min} \geq {1 \over 2} \times (V_O+V_d+V_{RL}) \times {T_{OFF(max)} \over I_{O(crit)}} \]

Ecuația de mai sus poate fi simplificată și asezată într-o formă mai ușor de folosit:

\[ L_{min} \geq {{V_O \times \left (1-{{V_O} \over V_{i(max)}} \right ) \times T_S} \over {2 \times I_{O(crit)}}} \]

Utilizarea valorii inductanței astfel calculate asigură funcționarea în modul continuu pentru curenții de sarcină/ieșire peste nivelul curentului critic, \(I_{O(crit)}\).

Calculul componentelor unui etaj de tip Buck

În cele ce urmează se va prezenta un algoritm de clacul în vederea dimensionării unui etaj de tip Buck ce va funcționa în regim de conducție continuu.

Figura 7. Schema de principiu al unui etaj Buck

Parametrii necesari (cunoscuți)

în vederea dimensionării unui etaj de tip Buck (ca în figura de mai sus) sunt necesari următorii patru parametri:

\(V_{IN_{(min)}}\) și \(V_{IN_{(max)}}\), domeniul tensiunii de intrare;
\(V_{OUT}\), tensiunea nominală de ieșire;
\(I_{OUT_{(max)}}\), curentul maxim de ieșire;
Fișa de catalog al CI-ului (circuitului integrat) folosit la construirea etajului Buck, din care se vor folosi anumiți parametri.

Determinarea curentului maxim de comutare

În vederea determinării curentului maxim de comutare este necesar mai întâi să determinăm factorul de umplere \(D\) pentru tensiunea maximă de intrare, deoarece aceasta impune evident curentul maxim de comutare:

\[ D={V_{OUT} \over {V_{IN_{(max)}} \cdot \eta}}\]

unde:
\(V_{OUT}\) - reprezintă tensiunea de ieșire;
\(V_{IN_{(max)}}\) - reprezintă tensiunea maximă de intrare;
\(\eta\) - reprezintă randamentul etajului Buck.

Este necesar a ține cont de randament, \(\eta\) , pentru a acoperi pierderile etajului de tip Buck. Când acesta nu este cunoscut, din foile de catalog, se poate estima că dacă considerăm un randament de 90% vom acoperi pierderile din cadrul etajului de tip Buck.

Următorul pas, în determinarea curentului maxim de comutare, este determinarea riplului de curent prin inductor. În fișa de catalog al convertorului este specificat, în mod normal, valoarea specifică a inductorului sau o serie de bobine (inductoare) ce pot fi folosite în utilizarea CI (circuitului integrat).
În determinarea riplului de curent (curent ondulator), prin inductor, vom folosi valoarea inductanței din mijlocul intervalului recomandat sau dacă nu este specificat acest parametru vom folosi valoarea determinată din secțiunea următoare - Alegerea inductorului.

\[ \Delta I_L = {({{V_{IN_{(max)}}-V_{OUT}}) \cdot D} \over {f_s \cdot L}}\]

unde:
\(V_{IN_{(max)}}\) - reprezintă tensiunea maximă de intrare;
\(V_{OUT}\) - reprezintă tensiunea dorită la ieșire;
\(D\) - factorul de umplere , determinată anterior;
\(f_s\) - frecvența minimă de comutare a convertorului;
\(L\) - valoarea inductanței bobinei (inductorului).

În cele ce urmează se va determina dacă circuitul integrat (CI-ul) ce conține \(SW\) poate furniza curentul maxim de ieșire (de comutare).

\[ I_{MAXOUT} = {I_{LIM_{(min)}}-{\Delta I_L \over 2}}\]

Dacă valoarea calculată a curentului maxim de ieșire, \(I_{MAXOUT}\), este mai mic decât curentul maxim de ieșire necesar, atunci vom crește frecvența de comutare, \(f_s\), pentru a reduce riplu de curent, \(\Delta I_L\), sau se va alege un comutator cu un curent mai mare de ieșire. Dacă curentul maxim de ieșire, \(I_{MAXOUT}\), este numai un pic mai mic decât curentul maxim de ieșire necesar, atunci vom crește inductanța bobinei (inductorului), \(L\), dacă ne aflăm în domeniul recomandat al inductorului. Se observă, din ecuația anterioară a riplului de curent \(\Delta I_L\), că prin mărirea inductanței, \(L\), sau mărirea frecvenței de comutare, \(f_s\), se poate micșora riplu de curent \(\Delta I_L\) și prin urmare se va crește curentul maxim de ieșire , \(I_{MAXOUT}\).
Dacă valoarea calculată a curentului maxim de ieșire, \(I_{MAXOUT}\), este peste valoarea maximă a curentului maxim necesar atunci valoarea maximă a curentului de comutație, \(I_{SW_{(max)}}\), se va calcula cu formula:

\[ I_{SW_{(max)}} = {\Delta I_L \over 2} + I_{OUT_{(max)}}\]

unde:
\(\Delta I_L\) - reprezintă riplu de curent prin bobină (inductor);
\(I_{OUT_{(max)}}\) - reprezintă curentul maxim necesar la ieșire.
\(I_{SW_{(max)}}\) - reprezintă curentul maxim de comutație, acesta fiind curentul de vârf la care va trebui să reziste elementul comutator, \(SW\), bobina, \(L\), și dioda, \(D\).

Alegerea inductorului

Fișele de catalog, a convertorului de tip Buck, oferă adesea o serie de valori recomandate ale inductorului. În acest caz putem alege bobina (inductorul) ca având o valoare a inductanței din lista de valori sau un model anume indicat. Din formulele anterioare se poate trage concluzia că, cu cât este mai mare valoarea inductanței a bobinei, \(L\), cu atât este mai mare valoarea curentului maxim de ieșire, \(I_{MAXOUT}\), ca urmare a reducerii riplului de curent, \(\Delta I_L\). De asemenea curentul maxim suportat de inductorul, \(L\), ales va trebui să fie mai mare ca valoarea curentului maxim de comutație, \(I_{SW_{(max)}}\).
Pentru cazurile în care nu avem specificat în foile de catalog o anumită listă de inductoare ecuația următoare poate fi folosită în alegerea inductanței necesare:

\[ L={{V_{OUT} \cdot (V_{IN} - V_{OUT})} \over {\Delta I_L \cdot f_s \cdot V_{IN}}}\]

unde:
\(V_{IN}\) - reprezintă tensiunea de intrare;
\(V_{OUT}\) - reprezintă tensiunea nominală de ieșire;
\(f_s\) - reprezintă frecvența de oscilație a convertorului;
\(\Delta I_L\) - reprezintă curentul de riplu estimat prin inductor.

Deoarece în acest caz nu cunoaștem \(L\) și nu putem determina \(\Delta I_L\), cu ajutorul formulei anterioare, atunci vom estima acesteia ca fiind:

\[ \Delta I_L={(0,2 \div 0,4) \cdot I_{OUT_{(max)}}}\]

unde:
\(\Delta I_L\) - reprezintă curentul de riplu estimat prin inductor;
\(I_{OUT_{(max)}}\) - reprezintă curentul maxim necesar la ieșire.

Alegerea diodei

Pentru reducerea pierderilor se vor utiliza diode Schottky.
Dioda va trebui să prezinte un curent în conducție directă, \(I_F\), egal cu maximul curentului de ieșire:

\[ I_F={I_{OUT_{(max)}} \cdot (1-D)}\]

unde:
\(I_F\) - reprezintă valoarea medie a curentului diodei în conducție directă;
\(I_{OUT_{(max)}}\) - reprezintă curentul maxim necesar la ieșire;
D - factorul de umplere.
Dioda Schottky aleasă va trebui să aibă curentul de vârf mai mare decât valoarea medie.

Un alt parametru ce va trebui calculat este puterea disipată de diodă, \(P_D\), astfel:

\[ P_D={I_F \cdot V_F}\]

unde:
\(I_F\) - reprezintă valoarea medie a curentului diodei în conducție directă;
\(V_F\) - reprezintă căderea de tensiune pe diodă, în conducție directă.

Valoarea tensiunii de ieșire

Aproximativ la toate convertoarele de tensiune (circuite integrate) tensiunea de ieșire este setată cu ajutorul unui divizor rezistiv (care este integrat în cazul convertoarelor cu tensiune fixă de ieșire).
Divizorul de tensiune poate fi calculat cu ajutorul tensiunii și curentului de feedback, \(V_{FB}\) respectiv \(I_{FB}\).

Figura 8. Divizorul rezistiv folosit la stabilirea tensiunii de ieșire

Curentul prin rezistorul rezistiv, \(I_{R12}\), va trebui să fie de cel puțin 100 de ori mai mare decât curentul de feedback, \(I_{FB}\):

\[ I_{R12} \geq {100 \cdot I_{FB}}\]

unde:
\(I_{FB}\) - reprezintă curentul de feedback, stabilit conform datelor de catalog; \(I_{R12}\) - reprezintă curentul prin divizorul rezistiv către masă.
Această impunere face ca să obținem o eroare mai mică de \(1%\) la măsurarea tensiunii iar curentul de feedback, \(I_{FB}\), poate fi neglijat.
Tinân cont de impunerea anterioară, rezistoarele vor fi calculate astfel:

\[ R_2={V_{FB} \over I_{R12}}\]

\[ R_1={R_2 \cdot ({V_{OUT} \over {V_{FB}}}-1)}\]

unde:
\(R_1\), \(R_2\) - reprezintă rezistențele divizorului de tensiune;
\(V_{FB}\) - reprezintă tensiunea de feedback, din datele de catalog;
\(I_{R12}\) - reprezintă curentul prin rezistorul rezistiv;
\(V_{OUT}\) - reprezintă tensiunea necesară de ieșire.

Alegerea condensatorului de la intrare

Valoarea minimă pentru condensatorul de intrare este, în mod normal, dată de fișa tehnică a convertorului.
Aceasta valoare minimă este necesară pentru a stabili tensiunea de intrare datorate cerinței de curent de vârf a sursei în comutație.
Cele mai bune sunt condensatoarele cu rezistența serie echivalentă, \(ESR\), mică, iar din această categorie fac parte condensatoarele ceramice.
În cazul în care tensiunea de intrare este zgomotoasă se poate mări această capacitate.

Alegerea condensatorului de la ieșire

Și în acest caz vom alege condensatorul cu \(ESR\) scăzut, iar în acest sens condensatoarele ceramice fiind o bună alegere.
Dacă convertorul este prevăzut cu compensator extern atunci orice valoare a capacității peste valoarea minimă recomandată de fișele de catalog poate fi folosită.
Următoarele ecuații pot fi folosite pentru alegerea condensatorului de ieșire pentru un riplu de tensiune dorit:

\[ C_{OUT_{min}}={\Delta I_{L} \over {8 \cdot f_s \cdot \Delta V_{OUT}}}\]

unde:
\(C_{OUT_{min}}\) - reprezintă capacitatea minimă a condensatorului de ieșire;
\(\Delta I_L\) - reprezintă curentul de riplu estimat prin inductor;
\(f_s\) - frecvența minimă de oscilație a convertorului;
\(\Delta V_{OUT}\) - riplu de tensiune la ieșire.
\(ESR\) adaugă și mai mult riplu, dat de ecuația:

\[ \Delta V_{OUT_{ESR}}={ESR \cdot \Delta I_L}\]

unde:
\(\Delta V_{OUT_{ESR}}\) - adaosul de riplu de tensiune datorat \(ESR\);
\(ESR\) - rezistența serie echivalentă aferent condensatorului;
\(\Delta I_L\) - reprezintă curentul de riplu prin inductor.
De cele mai multe ori alegerea capacității de ieșire se realizează în regimul tranzitoriu și nu cel static. Deviația tensiunii de ieșire este cauzată de timpul necesar inductorului de a răspunde la creșterea sau la scăderea curentului necesar.

\[ C_{OUT_{min}}={{\Delta I^2_{OUT} \cdot L} \over {2 \cdot V_{OUT} \cdot V_{OS}}}\]

unde:
\(C_{OUT_{min}}\) - reprezintă capacitatea minimă la ieșire pentru depășire;
\(\Delta I_{OUT}\) - reprezintă variația maximă a curentului de ieșire;
\(V_{OUT}\) - reprezintă tensunea dorită la ieșire;
\(V_{OS}\) - reprezintă tensiunea dorită la ieșire și modificată datorită depășirii ca urmare a regimului tranzitoriu.

Convertorul de c.c. ridicător - de tip Boost

În figura de mai jos este prezentată o schemă simplificată a convertorului de tip Boost cu un bloc de comandă inclus.
Schema prezintă un întreupător \(Q_1\) realizat cu ajutorul unui tranzistor MOSFET cu canal N, dioada, \(CR1\), un inductor (bobină) \(L\) și un condensator, \(C\), ce formează filtrul de ieșire. În analiză sunt luate în considerare rezistența serie echivalentă, \(ESR\), a condesatorului, notată cu \(Rc\) și rezistența în c.c. a inductorului (bobinei), \(L\), notată \(RL\). Rezistorul, \(R\), reprezintă sarcina văzută de către convertorul de tip Boost.

Figura 9. Schema electrică a unui convertor de c.c. de tip Boost.

Pentru analiză voi folosi un program de tip CAD, numit LTspice a celor de la Analog Devices.
Întrerupătorul de putere, \(Q1\), este un tranzistor MOSFET cu canal N, dioda, \(CR1\), este de obicei o diodă ce prezintă o cădere mică de tensiune, pentru a limita pierderile. Bobina \(L\) și condensatorul \(C\) formează filtrul de ieșire.

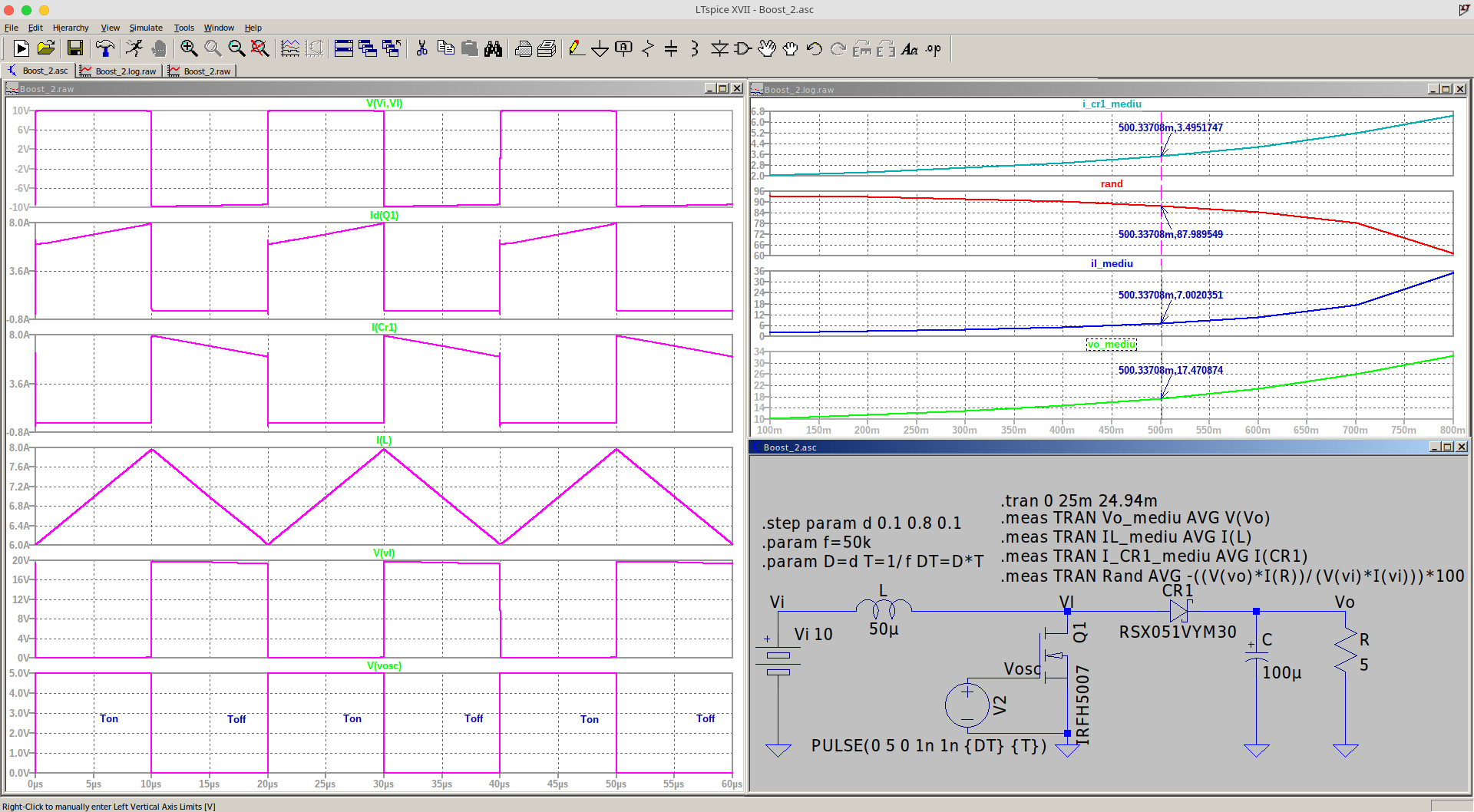Figura 9a. Schema electrică a unui convertor de c.c. de tip Buck, in vederea simulării cu LTspice.

Fișierul netlist al circuitului din Figura 9a este prezentat mai jos:

* C:\users\florin\Documentele mele\LTspiceXVII\Boost_2.asc
Vi Vi 0 10
M§Q1 Vl Vosc 0 0 IRFH5007
V2 Vosc 0 PULSE(0 5 0 1n 1n {DT} {T})
D§CR1 Vl Vo RSX051VYM30
L Vi Vl 50µ Ipk=7 Rser=0.02 Rpar=38000 Cpar=5.86p mfg="Gowanda" pn="894AT5002V"
C Vo 0 100µ V=25 Irms=370m Rser=0.24 Lser=0 mfg="Nichicon" pn="UPL1E101MPH" type="Al electrolytic"
R Vo 0 5
.model D D
.lib C:\users\florin\Documentele mele\LTspiceXVII\lib\cmp\standard.dio
.model NMOS NMOS
.model PMOS PMOS
.lib C:\users\florin\Documentele mele\LTspiceXVII\lib\cmp\standard.mos
.step param d 0.1 0.8 0.1
.param f=50k
.param D=d T=1/f DT=D*T
.meas TRAN Vo_mediu AVG V(Vo)
.meas TRAN IL_mediu AVG I(L)
.meas TRAN I_CR1_mediu AVG I(CR1)
.meas TRAN Rand AVG -((V(vo)*I(R))/(V(vi)*I(vi)))*100
.tran 0 25m 24.94m
.backanno
.end

În timpul funcționării normale a convertorului c.c. - c.c., de tip Boost, întrerupătorul \(Q1\) este comandat pe poziția închis, respectiv deschis de către circuitul/blocul de comandă. Acesta acțiune a circuitului/blocului de comandă asupra întrerupătorului determina apariția unui tren de impulsuri la intersecția celor trei elemente \(Q1\), \(CR1\) și \(L\). Chiar dacă inductorul \(L\) este conectat la condensatorul de ieșire, \(C\), numai atunci când dioda, \(CR1\), conduce, acesta (inductorul) formează împreună cu condensatorul de ieșire, \(C\), un filtru de ieșire \(L-C\) ce are ca scop filtrarea trenului de impulsuri în vederea producerii unei tensiuni continue de ieșire, \(V_o\).

Analiza în regim static (steady state) a convertorului c.c. - c.c. ridicător (de tip Boost)

Un astfel de convertor poate funcționa în modul curent discontinuu sau continuu (funcție de curentul prin bobina \(L\)).
Modul curent continuu este caracterizat de circulația continuă a curentului prin bobina \(L\) pe durata întregului ciclu de comutație.
Modul curent discontinuu este caracterizat de circulația întreruptă a curentului prin bobina \(L\), cu treceri prin zero. Acest mod este caracterizat prin faptul că, curentul prin bobină este zero pentru o porțiune a ciclului de comutare. Începe de la zero, atinge o valoare maximă și revine la zero în timpul fiecărui ciclu de comutare.
Aceste două moduri vor fi analizate detailat în cele ce urmează. Este de dorit ca un astfel de etaj să rămână, pe tot timpul funcționării, numai într-un singur mod deoarece răspunsul în frecvență al etajului se schimbă semnificativ între cele două moduri de funcționare.
Pentru acestă analiză este folosit un tranzistor MOSFET cu canal N, ce este comandat cu tensiune pozitivă \(V_{GS(ON)}\), aplicată pe poarta \(G\) și sursa \(S\) a tranzistorului/întrerupătorului \(Q1\) de către circuitul de comandă ce comandă pe poziția \(ON\) acest întrerupător/tranzistor \(Q1\). Avantajul acestui tranzistor MOSFET cu canal N, este că are mică rezistența în conducție \(R_{DS(ON)}\), dar circuitul de comandă este mai complicat. În cazul tranzistorului de tip MOSFET cu canal P ce are, în general, o rezistență în conducție \(R_{DS(ON)}\) mai ridicată, circuitul de comandă este mai simplu.
Tranzistorul \(Q1\) și dioda \(CR1\) sunt desenate, în Figura 9, în chenarul cu linie punctată, cu terminalele etichetate a, p și c. Curentul prin bobina \(L\) notat cu \(I_L\), este același cu curentul ce iese prin terminalul notat c, respectiv curentul \(i_c\).

Analiza în modul curent continuu a convertorului c.c. - c.c. ridicător (de tip Boost)

În cele urmează se descrie funcționarea etajului de tip Boost, în regim static (steady state), în modul curent continuu de funcționare (\(I_L>0\)).
Principalul rezultat al acestei analize este dependența tensiunii de ieșire \(V_o\) față de factorul de umplere \(D\) și a tensiunii de intrare \(V_i\), respectiv invers, factorul de umplere, \(D\), poate fi calculat pe baza tensiunii de ieșire, \(V_o\), respectiv de ieșire, \(V_i\).
Regimul static (steady state) implică faptul că tensiunea de intrare, tensiunea de ieșire, curentul de ieșire prin sarcină și factorul de umplere sunt fixe și nu variază. În general literele cu majusculă sunt atribuite numelor variabilelor pentru a indica o cantitate aflată în stare statică.
În modul de conducție continuu, etajul de tip Boost presupune două stări de comutare pe durata unui ciclu.

STAREA ON - atunci când tranzistorul/întrerupătorul, \(Q1\), este \(ON\) și \(CR1\) este \(OFF\);
STAREA OFF - atunci când tranzistorul/întrerupătorul, \(Q1\), este \(OFF\) și \(CR1\) este \(ON\).

Schemele electrice echivalente fiecărei stări sunt prezentate în figura de mai jos, Figura 10.

Figura 10. Stările \(ON\) și \(OFF\) a etajului de tip Boost.

Durata de timp a stării \(ON\) este:

\[ {T_{ON}}={D} \times {T_S}\]

, unde \(D\) este factorul de umplere, impus de blocul de comandă, exprimat ca raport al timpului când întrerupătorul este \(ON\) la durata de timp a întregii perioade, \(T_S\):

\[ {D} = {{T_{ON}} \over {T_{S}}}\]

\[ T_{OFF}=(1-D) \times T_S\]

, unde \((1-D)\) este notat uneori cu \(D'\).

Aceste cicluri de timp sunt prezentate în Figura 11.

Figura 11. Formele de undă în modul de conducție continuu, \(I_L>0\).

Dacă ne uităm la Figura 10, în timpul stării \(ON\), observăm că:

\(Q1\) prezintă o rezistență scăzută, \(R_{DS(ON)}\), de la drena \(D\) către sursa \(S\) și are o mică cădere de tensiune:
\[ V_{DS}=I_{L} \times R_{DS(ON)}\]
Există de asemnea, o cădere mică de tensiune pe rezistență în c.c. a bobinei/inductorului, \(L\), egală cu:
\[ V_{RL}=I_L \times R_L\]

Astfel tensiunea de intrare, \(V_i\), minus pierderile (\(V_{DS}+V_{RL}\)), este aplicată în partea stângă a bobinei/inductorului, \(L\). \(CR1\) este \(OFF\) în tot acest timp deoarece tensiunea aplicată este inversă. Tensiunea aplicată în partea dreaptă a bobinei/inductorului \(L\) este căderea de tensiune pe tranzistorul MOSFET, \(V_{DS}\).
Curentul prin bobină, \(I_L\), curge de la sursa de intrare, \(V_i\), prin \(Q1\) către masă.
În timpul stării \(ON\), tensiunea aplicată pe bobină, \(V_L\), este constantă și egală cu:

\[ V_L=V_i-V_{DS}- V_{RL}\]

Adoptând convenția de polaritate pentru curentul \(I_L\) prezentată în Figura 10, curentul prin bobină crește ca urmare a tensiunii aplicate. De asemenea deoarece tensiunea aplicată este în esență constantă, curentul prin bobină crește liniar.
Această creștere a curentului prin bobină în timpul \(T_{ON}\) este ilustrat în Figura 11.

\[ {V_L}={L} \times {{di} \over {dt}} \Rightarrow \Delta I_L = {V_L \over L} \times \Delta T\]

Creșterea curentului prin circuit, pe durata stării \(ON\), este dată de:

\[ \Delta I_L(+) = {{V_i - V_{DS} - V_{RL}} \over L} \times T_{ON}\]

Valoarea \(\Delta I_L(+)\) este riplu de curent prin bobină. Pe timpul acestei perioade, întregul curent de sarcină este asigurat de către condensatorul de ieșire, \(C\).

Dacă ne uităm la Figura 10, atunci când \(Q1\) este \(OFF\), acesta prezintă o impedanță ridicată între drena \(D\) și sursa \(S\). De aceea, deoarece curentul care circulă prin bobina/inductorul \(L\) nu se poate schimba instantaneu, curentul trece de la tranzistorul \(Q1\) la dioda \(CR1\). Odată cu scăderea curentului prin bobină, tensiunea pe bobină își inversează polaritatea până când dioda \(CR1\) devine polarizată direct și intră în conducție (\(ON\)).
Tensiunea în partea stângă a bobinei, \(L\), rămâne aceeași ca și înainte fiind \(V_i-V_{RL}\).
Tensiunea aplicată în partea dreaptă a bobinei, \(L\), este acum tensiunea de ieșire, \(V_O\), plus căderea de tensiune, în conducție directă, pe diodă, \(V_d\) .
Curentul prin bobină, \(I_L\), curge acum de la sursa de intrare, \(V_i\), prin dioda, \(CR1\), către ieșirea realizată din condensatorul \(C\) și rezistența de sarcină \(R\).
În timpul stării \(OFF\), tensiunea aplicată bobinei \(L\) este constantă și este egală cu:

\[ V_L = (V_O+V_d+V_{RL})-V_i\]

Menținând aceeași convenție de polaritate, acestă tensiune aplicată este negativă (sau opusă ca polaritate cu tensiunea aplicată în starea \(ON\)).
Prin urmare curentul prin bobină scade, în timpul stării \(OFF\).
De asemenea, deoarece tensiunea aplicată este în esență constantă, curentul prin bobină \(I_L\) va scade liniar. Acestă scădere a curentului \(I_L\) prin bobină în timpul stării \(OFF\) este prezentată de asemenea în Figura 11.
Curentul prin bobină, pe durata stării \(OFF\), va scade în conformitate cu relația:

\[ \Delta I_L(-)={{{(V_O+V_d+V_{RL})-V_i} \over {L}} \times T_{OFF}} \]

Valoarea \(\Delta I_L(-)\) este de asemenea riplu de curent prin bobină.

\[ V_O = {(V_i-V_{RL}) \times (1+{T_{ON} \over T_{OFF}})-V_d-V_{DS} \times {T_{ON} \over T_{OFF}}}\]

, unde:

\[ \left.\begin{matrix} {T_S=T_{ON}+T_{OFF}} \\ {D={T_{ON} \over T_S}} \\ {(1-D) = {T_{OFF} \over T_S}} \end{matrix}\right\} \Rightarrow V_O={{{V_i-V_{RL}} \over {1-D}}-V_d-V_{DS} \times {D \over {1-D}}}\]

În ecuațiile de mai sus ale \(\Delta I_L(+)\) și \(\Delta I_L(-)\), tensiunea de ieșire, \(V_O\), a fost implicit presupusă a fi constantă, fără riplu de tensiune pe durata \(ON\) sau \(OFF\).
Aceasta este o simplificare și implică două ipoteze separate:

în primul rând, se presupune condensatorul de ieșire, \(C\), ca fiind suficient de mare astfel încât riplu/schimbarea de tensiune este neglijabilă;
în al doilea rând, se presupune căderea de tensiune pe \(ESR\) (rezistența serie echivalentă \(R_C\)) este de asemenea neglijabilă.

Aceste ipoteze sunt valabile, deoarece valoarea riplului de tensiune este proiectată a fi mult mai mică decât valoarea tensiunii de ieșire, \(V_O\), în c.c..
Relația factorului de transformare a tensiunii de ieșire \(V_O\), de mai sus, ilustrează faptul că tensiunea de ieșire \(V_O\) poate fi modificată prin ajustarea/modificarea factorului de umplere \(D\) și este întotdeauna mai mare decât tensiunea de intrare \(V_i\) deoarece \(D\) satisface condiția \(0>D<1\).
O altă simplificare folosită este a considera \(V_{DS}\), \(V_d\) și \(R_L\) implicit și \(V_{RL}\) suficient de mici pentru a fi ignorate, astfel:

\[ \left.\begin{matrix} V_{DS}=0 \\ V_d = 0 \\ V_{RL} = 0 \end{matrix}\right\} \Rightarrow V_O = {{V_i} \over {1-D}}\]

O analiză simplificată a circuitului este de a considera bobina/inductorul, \(L\), un element de stocare a energiei.
Astfel când \(Q1\) este \(ON\) energia este adăugată bobinei/inductorului, \(L\), iar când \(Q1\) este \(OFF\) inductorul/bobina, \(L\), și sursa de alimentare, \(V_i\), livrează energie către condensatorul de ieșire, \(C\), și către sarcina, \(R\).
Tensiunea de ieșire, \(V_O\), este controlată prin setarea timpului de comandă (conducție) a lui \(Q1\). De exemplu prin creșterea timpului de conducție (a duratei \(ON\)) a lui \(Q1\) energia livrată către inductorul/bobina, \(L\), va crește, iar apoi mai multă energie va fi livrată către ieșire, pe durata \(OFF\), a lui \(Q1\), ceea ce va duce la creșterea tensiunii de ieșire \(V_O\).
Spre deosebire de etajul coborâtor (convertorul Buck), curentul mediu prin inductor/bobină, \(I_{L_{(med)}}\), nu va fi același cu, curentul de ieșire, \(I_O\), în conformitate cu Figurile 10 și 11.
Ce este important să reținem, este că în acest caz (convertorul Boost) bobina/inductorul, \(L\), furnizează curent la ieșire numai pe durata \(OFF\). Acest curent mediu, în timpul unui ciclu de comutare complet, este egal cu curentul de ieșire, deoarece curentul mediu prin condensatorul de ieșire, \(C\), trebuie să fie nul.
Relația dintre curentul mediu prin inductor/bobină, \(I_{L_{(med)}}\), și curentul de ieșire, \(I_O\), al convertorului ridicător ce lucrează în regim continuu este dată de:

\[ I_{L_{(med)}} \times {T_{OFF} \over T_S} = I_{L_{(med)}} \times (1-D) = I_O\]

\[ I_{L_{(med)}} ={{I_O} \over {1-D}}\]

O altă observație importantă este că, curentul mediu prin bobină/inductor, \(I_{L_{(med)}}\), este proporțional cu, curentul de ieșire, \(I_O\).
De exemplu dacă curentul prin bobină/inductor, \(I_{L_{(med)}}\), scade cu \(2[A]\), din cauza scăderii curentului de sarcină atunci și valorile minime, \(\Delta I_L(-)\), și maxime, \(\Delta I_L(+)\), ale curentului prin bobină/inductor scad cu \(2[A]\), evident presupunem că modul de conducție continuu este menținut.

Analiza în modul curent discontinuu a convertorului de c.c. - c.c. ridicător (de tip Boost)

În cele ce urmează se va analiza ce se întâmplă atunci când curentul prin sarcină este scăzut iar modul de conducție este schimbat din modul de conducție continuu în modul de conducție discontinuu. Ne reamintim că pentru modul de conducție continuu, curentul prin inductor/bobina, \(I_{L(med)}\), urmărește curentul de ieșire, \(I_O\), și dacă acesta din urmă scade atunci și curentul mediu prin inductor/bobină, \(I_{L(med)}\), va face la fel. În plus și vârfurile minime și maxime ale curentului inductor vor urma curentul mediu al bobinei/inductorului, \(I_{L(med)}\).
Dacă curentul prin sarcina de ieșire este redus, sub nivelul critic, curentul prin bobină va fi zero pentru o porțiune a ciclului de comutare. Acest lucru ar trebui să fie evident din formele de undă prezentate în Figura 11, deoarece amplitudinea vârf la vârf a riplului de curent \(\Delta I_L\) nu se modifică cu, curentul de ieșire prin sarcină. Într-un convertor/etaj de tip Boost dacă curentul prin bobină \(I_L\) încercă să scadă sub zero atunci se va opri la zero (datorită curgerii unidirecționale a curentului prin dioda \(CR1\)) și va rămâne acolo până la începutul unui nou ciclu de comutare.
Acest mod operare se numește mod conducție discontinuu. Un convertor/etaj de tip Boost ce operează în acest mod de conducție discontinuu are trei stări unice în timpul fiecărui ciclu de comutare, spre deosebire de cele două stări pentru modul de conducție continuu.
Starea curentului prin inductor/bobină, \(I_L\), în cazul în care convertorul/etajul de tip Boost este la limita dintre modul de conducție continuu și discontinuu este arătată în Figura 12. Se observă cum curentul prin bobină/inductor scade la zero și ciclu următor de comutare începe imediat după ce curentul ajunge la zero.

Figura 12. Limita dintre modul de conducție continuu și discontinuu.

Scăderea suplimentară a curentului de ieșire pune convertorul/etajul de tip Boost în modul de conducție discontinuu. Acest mod de conducție este ilustrat în Figura 13. Răspunsul în frecvență a convertorului/etajului de tip Boost în modul de conducție discontinuu este destul de diferit de răspunsul în frecvență în modul de conducție continuu. De asemenea, relația intrare-ieșire este destul de diferită, după cum se arată în cele ce urmează.

Figura 13. Modul de conducție discontinuu.

Înainte de a determina raportul de transformare/conversie a modului de conducție discontinuu, observăm că există trei stări unice pe care convertorul/etajul de tip Boost le realizează în timpul funcționării în modul discontinuu a curentului:

Starea \(ON\) este atunci când \(Q1\) este \(ON\) și \(CR1\) este \(OFF\);
Starea \(OFF\) este atunci când \(Q1\) este \(OFF\) și \(CR1\) este \(ON\);
Starea \(IDLE\) (așteptare) este atunci când \(Q1\) este \(OFF\) și \(CR1\) este \(OFF\);

Primele două stări sunt identice cu cele ale modului de conducție continuu și circuitele din Figura 10 sunt aplicabile mai puțin \(T_{OFF} \neq (1-D) \times T_S\). Restul de timp rămas este starea \(IDLE\). În plus vom putea omite: rezistența în c.c. \(R_L\) a bobinei/inductorului \(L\) implicit și căderea de tensiune pe aceasta \(V_{RL}\), căderea de tensiune pe diodă \(V_d\) și căderea de tensiune \(V_{DS}\) pe tranzistorul \(Q1\) în starea \(ON\), deoarece sunt suficient de mici pentru a le considera zero/nule.
Durata stării \(ON\) este:

\[ T_{ON} = D \times T_S\]

, unde:
\(D\) - reprezintă factorul de umplere stabilit de circuitul de comandă exprimat ca raportul dintre \(T_{ON}\) și durata unui ciclu complet \(T_S\), respectiv:

\[ D = {T_{ON} \over T_S}\]

Duarata stării \(OFF\) este:

\[ T_{OFF} = D_2 \times T_S\]

Durata stării \(IDLE\) este restul timpului de comutare și este:

\[ T_S-T_{ON}-T_{OFF} = D_3 \times T_S\]

aceste stări sunt prezentate în Figura 14.
Ecuațiile pentru creșterea curentului, \(\Delta I_L(+)\), prin bobina/inductorul \(L\) pe durata stării \(ON\) și ecuațiile pentru descreșterea curentului, \(\Delta I_L(-)\), prin bobina/inductorul \(L\) pe durata stării \(OFF\) sunt determinate în cele ce urmează.
Astfel, creșterea curentului \(\Delta I_L(+)\) prin bobina/inductorul \(L\), în timpul stării \(ON\), este dată de:

\[ \Delta I_L(+)={V_i \over L} \times {T_{ON}} = {V_i \over L} \times {D \times T_S} = I_{pk}\]

Magnitudinea riplului de curent, \(\Delta I_L(+)\), reprezintă de asemenea vârful de curent, \(I_{pk}\), deoarece în modul de conducție discontinuu, curentul pornește de la zero la începutul fiecărui ciclu.

Scăderea curentului \(\Delta I_L(-)\) prin bobina/inductorul \(L\), pe durata stării \(OFF\), este dată de:

\[ \Delta I_L(-)={{V_O-V_i} \over L} \times {T_{OFF}}={{{V_O - V_i} \over L} \times D_2 \times T_S} \]

Ca și în cazul modului de conducție continue curentul crește, \(\Delta I_L(+)\), în timpul duratei \(ON\) și curentul scade \(\Delta I_L(-)\) în timpul duratei \(OFF\), iar aceste creșteri respectiv scăderi ale curentului sunt egale.
Prin urmare aceste două ecuații pot fi egalizate și rezolvate, scoțând \(V_O\), pentru a obține prima dintre cele două ecuații care trebuie folosite pentru a obține/rezolva raportul de conversie/transformare a tensiunilor:

\[ V_O=V_i \times {{T_{ON} + T_{OFF}} \over {T_{OFF}}}=V_i \times {{D+D_2} \over {D_2}}\]

Curentul de ieșire, \(I_O\), ce reprezintă tensiunea de ieșire \(V_O\) împărțită la sarcina de ieșire \(R\), este:

\[ I_O={V_O \over R} = {{1 \over T_S} \times \left({1 \over 2} \times I_{pk} \times D_2 \times T_S \right)}\]

Înlocuind în ecuația de mai sus \(I_{pk}\) determinat mai devreme, va rezulta:

\[ I_O={V_O \over R}={ {1 \over T_S} \times \left[ {1 \over 2} \times \left( {V_i \over L} \times D \times T_S \right) \times D_2 \times T_S \right]} \]

\[ I_O={V_O \over R}={{V_i \times D \times D_2 \times T_S} \over {2 \times L}}\]

Astfel am obținut două ecuații, cea pentru curentul de ieșire, \(I_O\), și cea pentru tensiunea de ieșire, \(V_O\), amândouă cu termenii \(V_i\), \(D\) și \(D_2\).
Rezolvănd acum fiecare ecuație pentru \(D_2\) și egalăm cele două ecuații obținute. Ecuația rezultată va fi, o expresie pentru tensiunea de ieșire, \(V_O\).
Relația de conversie/transformare a tensiunii în modul de conducție discontinuu este dată de:

\[ V_O=V_i \times {{1+ \sqrt {1+{{4 \times D^2} \over K}}} \over 2}\]

, unde:

\[ K = {{2 \times L} \over {R \times T_S}}\]

Relația de mai sus prezintă una dintre diferențele majore dintre cele două moduri de conducție. Pentru modul de conducție discontinuu, relația de transformare/conversie a tensiunii de ieșire, \(V_O\), este o funcție a tensiune de intrare, \(V_i\), a factorului de umplere, \(D\), a inductanței \(L\), a frecvenței de comutare \(T_S\) și a rezistenței de sarcină \(R\), în timp ce pentru modul de conducție continuu relația de transformare/conversie a tensiunii de ieșire depinde numai de tensiunea de intrare, \(V_i\), și de factorul de umplere, \(D\).

Figura 14. Formele de undă în modul de conducție discontinuu

În aplicațiile obișnuite, etajul de tip Boost, este operat fie în modul de conducție continuu fie în modul de conducție discontinuu. Pentru o anumită aplicație se alege un singur mod de funcționare iar etajul este astfel proiectat pentru a menține același mod.
În secțiunea următoare vom determina relațiile necesare pentru alegerea bobinei/inductorului care să permită funcționarea circuitului într-un singur mod de conducție.

Inductanță critică

Analizele anterioare, ale etajului de tip Boost, au fost pentru modurile de conducție continuu și discontinuu în regim static.
Modul de conducție al etajului este o funcție a tensiunii de intrare, tensiunii de ieșire, curentului de ieșire si a valorii inductanței aferente bobinei de la ieșire.
Un etaj de tip Boost poate fi proiectat să funcționeze în regim continuu, pentru curenți de sarcină peste un anumit nivel, de obicei 5%-10% din valoarea maximă.
De obicei, intervalul tensiunii de intrare, tensiunea de ieșire și curentul de sarcină sunt parametri impuși (definiți) ale etajului de tip Boost, urmând ca valoarea inductorului să fie un parametru ce urmează a fi determinat astfel încât să fie menținut mediul de regim continuu.
Valoarea minima a inductorului pentru a menține regimul de conducție continuu poate fi determinată urmând următorul algoritm.
Pentru început definim \(I_{O(crit)}\) ca fiind curentul minim pentru care încă se poate menține modul de funcționare continuu, prezentat în Figura 12.

\[ I_{L(min-mediu)}= {{\Delta I_L} \over {2}}\]

După care determinăm inductanța minimă a bobinei/inductorului care să satisfacă relația de mai sus, astfel:

\[ L_{min} \geq {1 \over 2} \times (V_i+V_{DS}-V_{RL}) \times {T_{ON} \over I_{L(min)}} \]

Ecuația de mai sus poate fi simplificată și asezată într-o formă mai ușor de folosit:

\[ L_{min} \geq {{V_O \times T_S} \over {16 \times I_{O(crit)}}} \]

Utilizarea valorii inductanței astfel calculate asigură funcționarea în modul continuu pentru curenții de sarcină/ieșire peste nivelul curentului critic, \(I_{O(crit)}\).

Calculul componentelor unui etaj de tip Boost

În cele ce urmează se va prezenta un algoritm de clacul în vederea dimensionării unui etaj de tip Boost ce va funcționa în regim de conducție continuu.

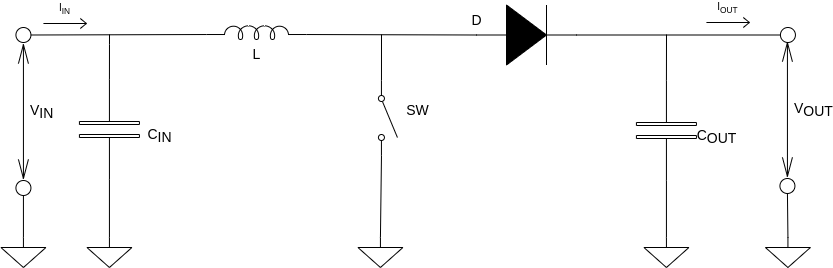
Figura 15. Schema de principiu al unui etaj Boost

Parametrii necesari (cunoscuți)

în vederea dimensionării unui etaj de tip Boost (ca în figura de mai sus) sunt necesari următorii patru parametri:

\(V_{IN_{(min)}}\) și \(V_{IN_{(max)}}\), domeniul tensiunii de intrare;
\(V_{OUT}\), tensiunea de ieșire;
\(I_{OUT_{(max)}}\), curentul maxim de ieșire;
Fișa de catalog al CI-ului (circuitului integrat) folosit la construirea etajului Boost, din care se vor folosi anumiți parametri.

Determinarea curentului maxim de comutare

În vederea determinării curentului maxim de comutare este necesar mai întâi să determinăm factorul de umplere \(D\) pentru tensiunea minimă de intrare, deoarece aceasta impune curentul maxim de comutare:

\[ D={1-{{V_{IN_{(min)}} \cdot \eta} \over V_{OUT}}}\]

unde:
\(V_{OUT}\) - reprezintă tensiunea de ieșire;
\(V_{IN_{(min)}}\) - reprezintă tensiunea minimă de intrare;
\(\eta\) - reprezintă randamentul etajului Boost.

Este necesar a ține cont de randament, \(\eta\) , pentru a acoperi pierderile etajului de tip Boost. Când acesta nu este cunoscut, din foile de catalog, se poate estima că dacă considerăm un randament de 85% vom acoperi pierderile din cadrul etajului de tip Boost.

Următorul pas, în determinarea curentului maxim de comutare, este determinarea riplului de curent prin bobină/inductor. În fișa de catalog al convertorului este specificat, în mod normal, valoarea specifică a bobinei/inductorului sau o serie de bobine/inductoare ce pot fi folosite în utilizarea CI (circuitului integrat).
În determinarea riplului de curent (curent ondulator), prin bobină/inductor, vom folosi valoarea inductanței din mijlocul intervalului recomandat sau dacă nu este specificat acest parametru vom folosi valoarea determinată din secțiunea următoare - Alegerea inductorului.

\[ \Delta I_L = {{{V_{IN_{(min)}}} \cdot D} \over {f_s \cdot L}}\]

unde:
\(V_{IN_{(min)}}\) - reprezintă tensiunea minimă de intrare;
\(D\) - factorul de umplere , determinat anterior;
\(f_s\) - frecvența minimă de comutare a convertorului;
\(L\) - valoarea inductanței bobinei/inductorului.

În cele ce urmează se va determina dacă circuitul intergrat (CI-ul) ce conține \(SW\) poate furniza curentul maxim de ieșire (de comutare).

\[ I_{MAXOUT} = {(I_{LIM_{(min)}}-{\Delta I_L \over 2}) \cdot (1-D)}\]

unde:
\(I_{LIM_{(min)}}\) - reprezintă valoarea minimă a curentului limită aferent elementului de comutație \(SW\), din datele de catalog;
\(\Delta I_L\) - reprezintă riplu de curent, calculat anterior;
\(D\) - reprezintă factorul de umplere, calculat anterior.
Dacă valoarea calculată a curentului maxim de ieșire, \(I_{MAXOUT}\), este mai mică decât a curentului maxim de ieșire necesar, atunci vom crește frecvența de comutare, \(f_s\), pentru a reduce riplu de curent, \(\Delta I_L\), sau se va alege un comutator cu un curent mai mare de ieșire. Dacă curentul maxim de ieșire, \(I_{MAXOUT}\), este numai un pic mai mic decât curentul maxim de ieșire necesar, atunci vom crește inductanța bobinei/inductorului, \(L\), dacă ne aflăm în domeniul recomandat al inductorului. Se observă, din ecuația anterioară a riplului de curent \(\Delta I_L\), că prin mărirea inductanței, \(L\), sau mărirea frecvenței de comutare, \(f_s\), se poate micșora riplu de curent \(\Delta I_L\) și prin urmare se va crește curentul maxim de ieșire , \(I_{MAXOUT}\).
Dacă valoarea calculată a curentului maxim de ieșire, \(I_{MAXOUT}\), este peste valoarea maximă a curentului maxim necesar atunci valoarea maximă a curentului de comutație, \(I_{SW_{(max)}}\), se va calcula cu formula:

\[ I_{SW_{(max)}} = {{\Delta I_L \over 2} + {I_{OUT_{(max)}} \over {1-D}}}\]

unde:
\(\Delta I_L\) - reprezintă riplu de curent prin bobină/inductor;
\(I_{OUT_{(max)}}\) - reprezintă curentul maxim necesar la ieșire;
\(D\) - reprezintă factorul de umplere;
\(I_{SW_{(max)}}\) - reprezintă curentul maxim de comutație, acesta fiind curentul de vârf la care va trebui să reziste elementul comutator, \(SW\), bobina, \(L\), și dioda, \(D\).

Alegerea inductorului

Fișele de catalog, a convertorului de tip Boost, oferă adesea o serie de valori recomandate ale inductorului. În acest caz putem alege bobina/inductorul ca având o valoare a inductanței din lista de valori sau un model anume indicat. Din formulele anterioare se poate trage concluzia că, cu cât este mai mare valoarea inductanței a bobinei/inductorului, \(L\), cu atât este mai mare valoarea curentului maxim de ieșire, \(I_{MAXOUT}\), ca urmare a reducerii riplului de curent, \(\Delta I_L\). De asemenea curentul maxim suportat de bobina/inductorul, \(L\), aleasă/ales, va trebui să fie mai mare ca valoarea curentului maxim de comutație, \(I_{SW_{(max)}}\).
Pentru cazurile în care nu avem specificat în foile de catalog o anumită listă de bobine/inductoare ecuația următoare poate fi folosită în alegerea inductanței necesare:

\[ L={{V_{IN} \cdot (V_{OUT} - V_{IN})} \over {\Delta I_L \cdot f_s \cdot V_{OUT}}}\]

unde:
\(V_{IN}\) - reprezintă tensiunea de intrare;
\(V_{OUT}\) - reprezintă tensiunea de ieșire;
\(f_s\) - reprezintă frecvența de oscilație a convertorului;
\(\Delta I_L\) - reprezintă curentul de riplu estimat prin inductor.

Deoarece în acest caz nu cunoaștem \(L\) și nu putem determina \(\Delta I_L\), cu ajutorul formulei anterioare, atunci vom estima acesteia ca fiind:

\[ \Delta I_L={(0,2 \div 0,4) \cdot I_{OUT_{(max)}} \cdot {V_{OUT} \over V_{IN}}}\]

unde:
\(\Delta I_L\) - reprezintă curentul de riplu estimat prin inductor;
\(I_{OUT_{(max)}}\) - reprezintă curentul maxim necesar la ieșire;
\(V_{OUT}\) - reprezintă tensiunea de ieșire;
\(V_{IN}\) - reprezintă tensiunea de intrare.

Alegerea diodei

Pentru reducerea pierderilor se vor utiliza diode Schottky.
Dioda va trebui să prezinte un curent în conducție directă, \(I_F\), egal cu maximul curentului de ieșire:

\[ I_F={I_{OUT_{(max)}}}\]

unde:
\(I_F\) - reprezintă valoarea medie a curentului diodei în conducție directă;
\(I_{OUT_{(max)}}\) - reprezintă curentul maxim necesar la ieșire.
Dioda Schottky aleasă va trebui să aibă curentul de vârf mai mare decât valoarea medie.

Un alt parametru ce va trebui calculat este puterea disipată de diodă, \(P_D\), astfel:

\[ P_D={I_F \cdot V_F}\]

unde:
\(I_F\) - reprezintă valoarea medie a curentului diodei, în conducție directă;
\(V_F\) - reprezintă căderea de tensiune pe diodă, în conducție directă.

Valoarea tensiunii de ieșire

Figura 16. Divizorul rezistiv folosit la stabilirea tensiunii de ieșire

Curentul prin rezistorul rezistiv, \(I_{R12}\), va trebui să fie de cel puțin 100 de ori mai mare decât curentul de feedback, \(I_{FB}\):

\[ I_{R12} \geq {100 \cdot I_{FB}}\]

unde:
\(I_{FB}\) - reprezintă curentul de feedback, stabilit conform datelor de catalog;
\(I_{R12}\) - reprezintă curentul prin divizorul rezistiv către masă.
Această impunere face ca să obținem o eroare mai mică de \(1\%\) la măsurarea tensiunii iar curentul de feedback, \(I_{FB}\), poate fi neglijat.
Ținând cont de impunerea anterioară, rezistoarele vor fi calculate astfel:

\[ R_2={V_{FB} \over I_{R12}}\]

\[ R_1={R_2 \cdot \left({V_{OUT} \over {V_{FB}}}-1 \right)}\]

Alegerea condensatorului de la intrare

Alegerea condensatorului de la ieșire

\[ C_{OUT_{min}}={{I_{OUT_{(max})} \cdot D} \over {f_s \cdot \Delta V_{OUT}}}\]

unde:
\(C_{OUT_{min}}\) - reprezintă capacitatea minimă a condensatorului de ieșire;
\(I_{OUT_{(max})}\) - reprezintă curentul maxim de ieșire;
\(D\) - reprezintă factorul de umplere;
\(f_s\) - frecvența minimă de oscilație a convertorului;
\(\Delta V_{OUT}\) - riplu de tensiune la ieșire.
\(ESR\) adaugă și mai mult riplu, dat de ecuația:

\[ \Delta V_{OUT_{ESR}}={ESR \cdot \left( {{I_{OUT_{(max})} \over {1-D}}+{{\Delta I_L} \over 2}}\right)}\]

unde:
\(\Delta V_{OUT_{ESR}}\) - adaosul de riplu de tensiune, datorat \(ESR\);
\(ESR\) - rezistența serie echivalentă, aferentă condensatorului;
\(D\) - reprezintă factorul de umplere, calculat anterior;
\(\Delta I_L\) - reprezintă curentul de riplu prin inductor, determinat anterior.

Rogers, Everett; Texas Instruments, „Understanding Buck Power Stages in Switchmode Power,” Martie 1999. [Interactiv]. Available: http://www.ti.com/lit/an/slva057/slva057.pdf ↩ ↩ ↩

Regulatorul de încărcare

Convertorul c.c. - c.c.

Convertorul de c.c. coborâtor - de tip Buck1

Analiza în regim static (steady state) a convertorului c.c. - c.c. coborâtor (de tip Buck)

Analiza în modul curent continuu a convertorului c.c. - c.c. coborâtor (de tip Buck)

Analiza în modul curent discontinuu a convertorului de c.c. - c.c. coborâtor (de tip Buck)

Inductanță critică

Calculul componentelor unui etaj de tip Buck

Parametrii necesari (cunoscuți)

Determinarea curentului maxim de comutare

Alegerea inductorului

Alegerea diodei

Valoarea tensiunii de ieșire

Alegerea condensatorului de la intrare

Alegerea condensatorului de la ieșire

Convertorul de c.c. ridicător - de tip Boost

Analiza în regim static (steady state) a convertorului c.c. - c.c. ridicător (de tip Boost)

Analiza în modul curent continuu a convertorului c.c. - c.c. ridicător (de tip Boost)

Analiza în modul curent discontinuu a convertorului de c.c. - c.c. ridicător (de tip Boost)

Inductanță critică

Calculul componentelor unui etaj de tip Boost

Parametrii necesari (cunoscuți)

Determinarea curentului maxim de comutare

Alegerea inductorului

Alegerea diodei

Valoarea tensiunii de ieșire

Alegerea condensatorului de la intrare

Alegerea condensatorului de la ieșire

Convertorul de c.c. coborâtor - de tip Buck¹